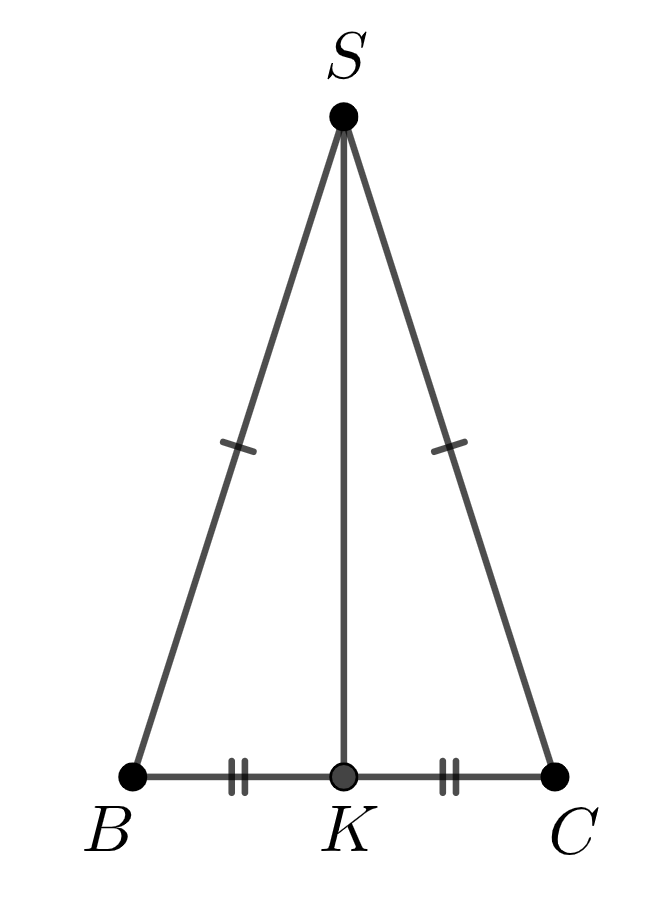
\(\displaystyle SABC\) дұрыс үшбұрышты пирамидада \(\displaystyle K\) – нүктесі \(\displaystyle BC{\small }\) қабырғасының ортасы \(\displaystyle S\) – төбесі. \(\displaystyle SK = 4{\small }\) және \(\displaystyle AC=9{\small }\) екені белгілі. Пирамиданың бүйір бетінің ауданын табыңыз.
1-тәсіл
Есеп шартында дұрыс пирамиданың бүйір бетінің ауданы \(\displaystyle S_{ бүй }\) берілген. Бұл аудан барлық бүйір жақтарының аудандарының қосындысы болып табылады.
Дұрыс пирамиданың бүйір жақтары – тең үшбұрыштар. Демек, бүйір жақтарының аудандары тең.
Дұрыс үшбұрышты пирамиданың үш бүйір жағы бар. Яғни,
\(\displaystyle S_{бүй}=S_{жақт}+S_{жақт}+S_{жақт}=3S_{жақт}\small. \)
\(\displaystyle S_{жақт}\small \) табайық
Төмендегіні аламыз:
\(\displaystyle S_{бүй}=3 \cdot S_{жақт}=3\cdot 18 = 54\small. \)
2-тәсіл
Пирамиданың бүйір бетінің ауданын есептеу үшін формуланы қолданайық.
Дұрыс пирамиданың бүйір бетінің ауданы
Дұрыс пирамиданың бүйір бетінің ауданы \(\displaystyle S_{ бүй }\)апофемаға табан периметрінің көбейтіндісінің жартысына тең.
\(\displaystyle S_{бүй}=\frac{1}{2}P_{осн} \cdot l{ \small ,} \)
мұндағы\(\displaystyle P_{табан } \) - табан периметрі,
\(\displaystyle l\) - апофема.
Дұрыс үшбұрышты пирамиданың табанының периметрі
\(\displaystyle P_{осн}=3\cdot AC{\small }\) тең.
Табылған \(\displaystyle P_{таб}\) және \(\displaystyle l\) мәндерін \(\displaystyle S_{ бүй }\)арналған формулаға алмастырайық.
\(\displaystyle S_{бүй }=\frac{1}{2}P_{табан } \cdot l{ \small ,} \)
\(\displaystyle S_{бүй}=\frac{1}{2}\cdot 3 \cdot AC \cdot SK{ \small .} \)
\(\displaystyle AC\) және \(\displaystyle SK{\small }\) мәндерін қояйық
\(\displaystyle S_{бүй}=\frac{1}{2}\cdot 3 \cdot 9 \cdot 4=54{ \small .}\)
Жауабы: \(\displaystyle 54{\small .}\)