Қабырғалары \(\displaystyle 5\) және \(\displaystyle 4\) және ауданы \(\displaystyle 10\) болатын параллелограмның сүйір бұрышын табыңыз.
Параллелограмның қабырғалары \(\displaystyle AB=4\) және \(\displaystyle AD=5 \small,\) \(\displaystyle \angle BAD\) – параллелограмның сүйір бұрышы болсын.
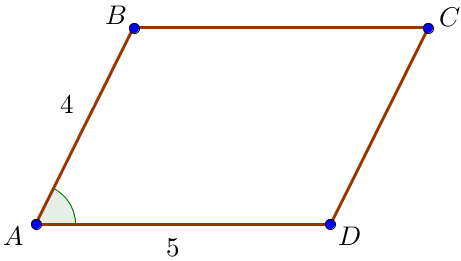
Параллелограмның ауданын көрші қабырғалар мен олардың арасындағы бұрыштың синусының көбейтіндісі ретінде табуға болады:
\(\displaystyle {S_{пар}} = {AB}\cdot AD \cdot \sin \angle BAD {\small.}\)
Осы мәндерді параллелограммның ауданын есептеу формуласына ауыстырыңыз:
\(\displaystyle 10 = 4\cdot 5 \cdot \sin \angle BAD {\small ,}\)
\(\displaystyle 10 = 20 \cdot \sin \angle BAD {\small ,}\)
\(\displaystyle \sin \angle BAD =\frac{1}{2}{\small.}\)
\(\displaystyle \angle BAD \) – сүйір болғандықтан \(\displaystyle \angle BAD =30^{\circ} {\small.}\)
Жауабы: \(\displaystyle 30^{\circ} {\small .}\)