Параллелограмның биіктіктері \(\displaystyle 9\) және \(\displaystyle 15 .\) Осы биіктіктердің біріншісі түсірілген қабырғасы \(\displaystyle 10 .\) Параллелограммның екінші қабырғасын табыңыз.

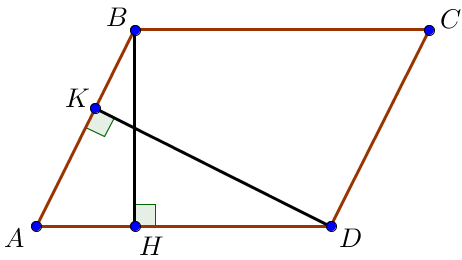
Параллелограмның биіктіктері \(\displaystyle BH=9\) және \(\displaystyle DK=15 \small,\) қабырғасы \(\displaystyle AD=10 {\small }\) болсын
Алдымен параллелограмның ауданын табыңыз. Параллелограммның ауданын табанының және биіктігінің көбейтіндісі ретінде табуға болады:
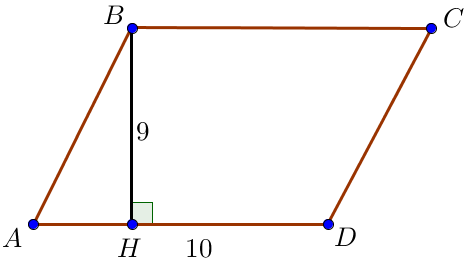
\(\displaystyle {S_{пар}} = {AD}\cdot BH = {10}\cdot 9 = 90 {\small.}\)
Басқа жақтан,
\(\displaystyle {S_{пар}} = {AB}\cdot DK {\small.}\)
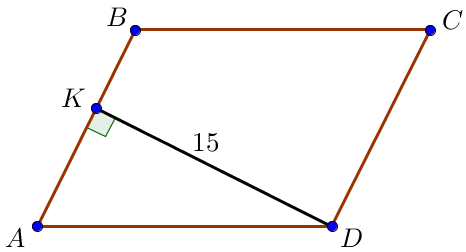
Демек,
\(\displaystyle 90 = {AB}\cdot 15 {\small ,}\)
\(\displaystyle AB = \frac{90}{15}=6 {\small .}\)
Жауабы: \(\displaystyle 6{\small .}\)