Skip to main content

Теориясы: Ортаңғы сызық

Тапсырма

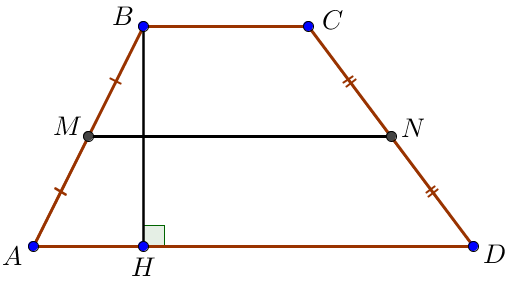
Табандары \(\displaystyle AD=16\) және \(\displaystyle BC=12\) болатын \(\displaystyle ABCD\) трапециясының \(\displaystyle MN\) орта сызығын сызыңыз. Егер \(\displaystyle AMND\) төртбұрышының ауданы \(\displaystyle 75\) болса, трапецияның биіктігін табыңыз.

Шешім

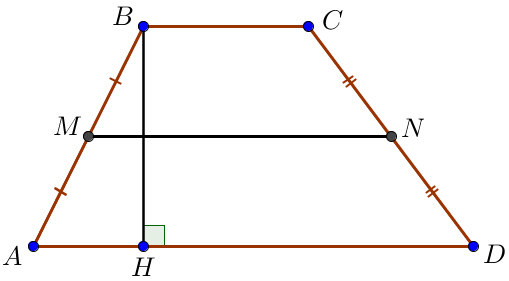
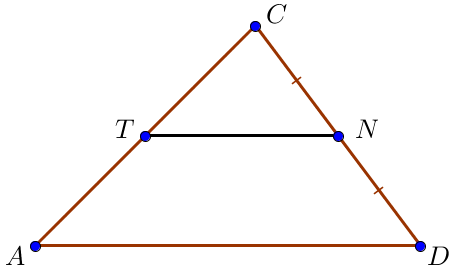
Трапецияның орта сызығы табандарының қосындысының жартысы болғандықтан, демек

\(\displaystyle MN=\frac{AD+BC}{2}=\frac{16+12}{2}=\frac{28}{2}=14\small.\)

 \(\displaystyle AMND\small\\ \) төртбұрышын қарастырайық.  Ондағы \(\displaystyle MN\) және \(\displaystyle AD\) қабырғалары трапецияның орта сызығының қасиеті бойынша параллель, \(\displaystyle AM\) және \(\displaystyle DN\) түзулері параллель емес, өйткені оларда бастапқы трапецияның қабырғалары бар.

Сонымен \(\displaystyle AMND\) төртбұрышы трапеция болып табылады.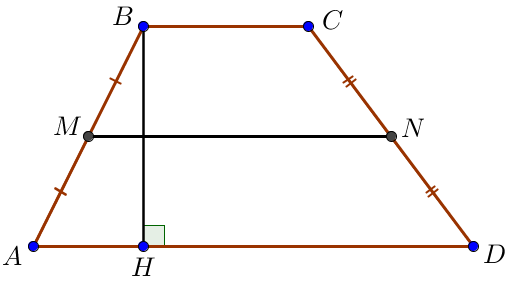 

 

\(\displaystyle BH\) –  \(\displaystyle ABCD\small\) трапециясының биіктігі болсын

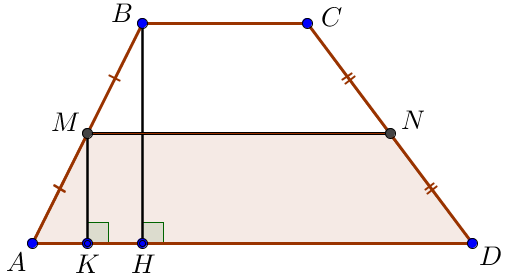
 \(\displaystyle ABH\small\) үшбұрышын қарастырайық

   \(\displaystyle AH\small\) кесіндінің ортасын  \(\displaystyle K\) 

Сонда \(\displaystyle MK\)  \(\displaystyle ABH\small\) үшбұрышының орта сызығы

Үшбұрыштың орта сызығының қасиеті бойынша:

  • \(\displaystyle MK=\frac{BH}{2}\small,\) 
  • \(\displaystyle MK\parallel BH\small,\) сондықтан\(\displaystyle MK\perp AD\small.\)

 

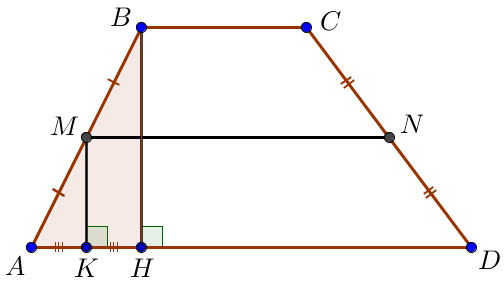 \(\displaystyle MK\)  \(\displaystyle AMND\small\)  трапециясының биіктігі болғандықтан

демек 

\(\displaystyle S_{AMND}=\frac{AD+MN}{2}\cdot MK\)

және

\(\displaystyle S_{AMND}=75\small,\)

 

\(\displaystyle \frac{AD+MN}{2}\cdot MK=75\small,\)

одан

\(\displaystyle \frac{16+14}{2}\cdot MK=75\small,\)

\(\displaystyle \frac{30}{2}\cdot MK=75\small,\)

\(\displaystyle 15\cdot MK=75\small,\)

\(\displaystyle MK=\frac{75}{15}=5\small.\)

бұдан

\(\displaystyle BH=MK\cdot 2=5\cdot 2=10\small.\)

Жауабы: \(\displaystyle 10{\small .}\)

Басқа шешім.