Табандары \(\displaystyle AD=16\) және \(\displaystyle BC=12\) болатын \(\displaystyle ABCD\) трапециясына \(\displaystyle MN\) орта сызығын сызыңыз. \(\displaystyle MB\) және \(\displaystyle CN\small\) кесінділердің ортаңғы нүктелерінің арасындағы қашықтықты табыңыз.
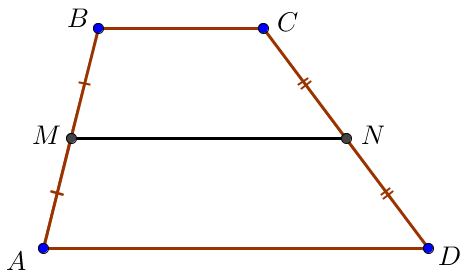
Трапецияның орта сызығы табандарының қосындысының жартысы болғандықтан, демек
\(\displaystyle MN=\frac{AD+BC}{2}=\frac{16+12}{2}=\frac{28}{2}=14\small.\)
Трапецияның орта сызығының қасиетін қолданайық.
Трапецияның орта сызығының қасиеті
Трапецияның орта сызығы трапеция табандарына параллель.
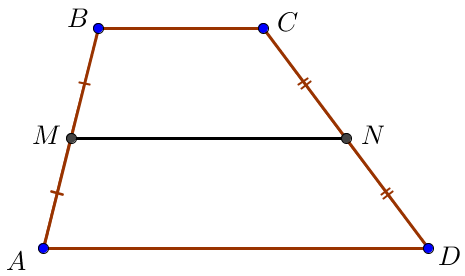
\(\displaystyle MN\parallel BC\parallel AD\)
Сонда \(\displaystyle MBCN\) төртбұрышында \(\displaystyle MN\) және \(\displaystyle BC\) қабырғалары параллель, бірақ \(\displaystyle MB\) және \(\displaystyle NC\) түзулері параллель емес, себебі олар бастапқы трапецияның бүйір қабырғалары.
Сонымен \(\displaystyle MBCN\) төртбұрышы трапеция болып табылады.
Тапсырма \(\displaystyle MBCN\) трапецияның орта сызығын \(\displaystyle m\) табу
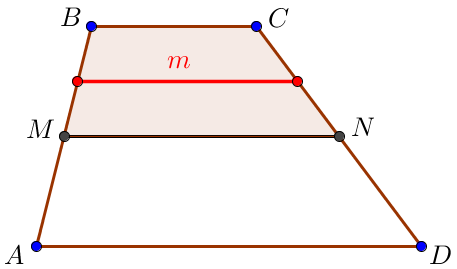
Трапецияның орта сызығын табандарының қосындысының жартысы болғандықтан, демек
\(\displaystyle m=\frac{MN+BC}{2}=\frac{14+12}{2}=\frac{26}{2}=13\small.\)
Жауабы: \(\displaystyle 13{\small .}\)