Доғал бұрыштың төбесінен тең қабырғалы трапецияның үлкен табанына түсірілген биіктік оны \(\displaystyle 10\) және \(\displaystyle 4\) тең кесінділерге бөледі. Осы трапецияның орта сызығын табыңыз.
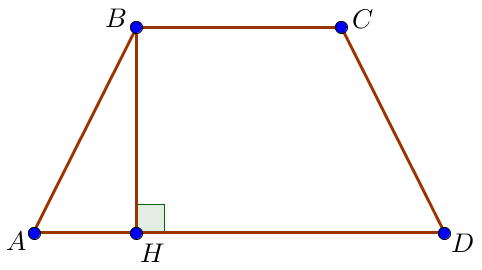
Трапецияның кіші \(\displaystyle BC\) және \(\displaystyle AD\) – үлкен табандары болсын, \(\displaystyle BH_1\) және \(\displaystyle CH_2\) – трапецияның биіктіктері. Биіктігі \(\displaystyle BH_1\) негізді \(\displaystyle AD\) кесінділерге \(\displaystyle AH_1=4\) және \(\displaystyle H_1D=10\small\) бөлсін. Біз алып жатырмыз: \(\displaystyle AD=AH_1+H_1D=\) \(\displaystyle =4+10=14\small.\) | 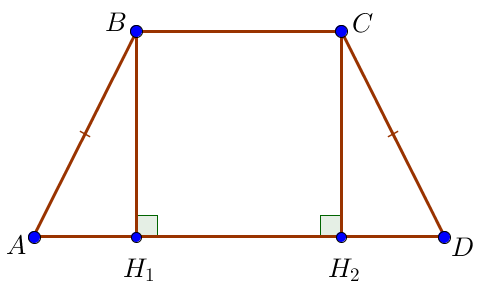 |
Тікбұрышты үшбұрыштар \(\displaystyle ABH_1\) және \(\displaystyle DCH_2\) гипотенузада \(\displaystyle AB=CD\) және катетінде \(\displaystyle BH_1=CH_2\small\) тең. Содан кейін \(\displaystyle DH_2=AH_1=4\) \(\displaystyle H_1H_2=10-4=6\small.\) | 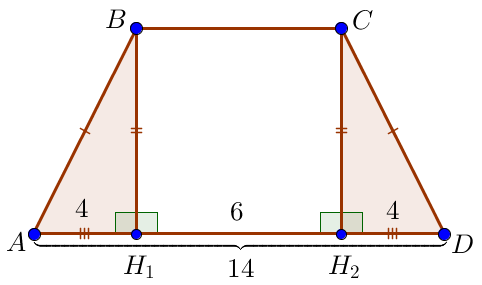 |
Төртбұрышта \(\displaystyle H_1BCH_2\) барлық бұрыштар тік. Демек, бұл тіктөртбұрыш. Демек,
\(\displaystyle BC=H_1H_2=6\small.\)
Трапецияның орта сызығының қасиетіне сәйкес,
\(\displaystyle m=\frac{BC+AD}{2}\small,\)
мұндағы \(\displaystyle m\) – трапецияның орта сызығы. Содан кейін
\(\displaystyle m=\frac{BC+AD}{2}=\frac{6+14}{2}=\frac{20}{2}=10\small.\)
Жауабы: \(\displaystyle 10{\small .}\)