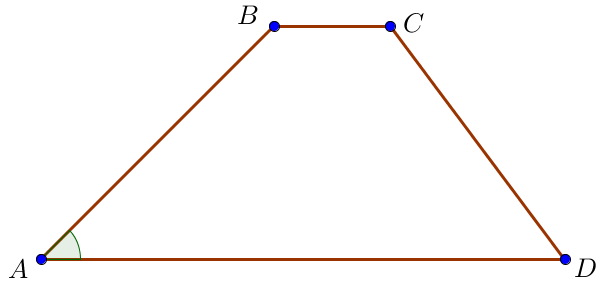
Трапецияның \(\displaystyle ABCD\) табандары \(\displaystyle AD=17\) және \(\displaystyle BC=3\small,\) белгілі \(\displaystyle AB=8\sqrt{2}\) және бұрышы \(\displaystyle \angle BAD=45^{\circ}\small.\) Трапецияның қабырғасын \(\displaystyle CD\) табыңыз.
Трапецияның биіктіктерін \(\displaystyle BH=CK\) сызыңыз. Трапецияның табандары параллель және трапецияның биіктіктері табандарына перпендикуляр болғандықтан , \(\displaystyle BH K C \) – тік төртбұрыш. Сонда \(\displaystyle H K = BC= 3\small .\) | 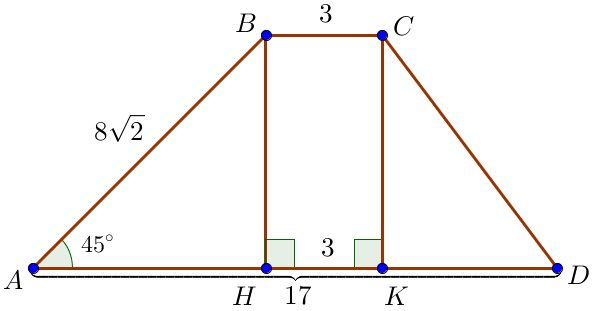 |
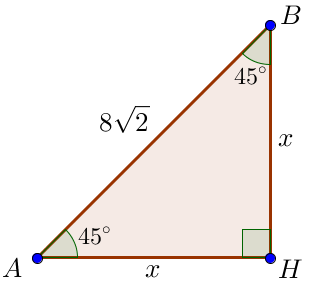
\(\displaystyle ABH\small\) тікбұрышты үшбұрышты қарастырайық
Біз сүйір бұрышты \(\displaystyle \angle BAH=45^{\circ}\) және гипотенузаны \(\displaystyle AB=8\sqrt{2}\small\) білеміз.
\(\displaystyle \angle ABH=180^{\circ}-\angle BAH-\angle AHB=180^{\circ}-45^{\circ}-90^{\circ}=45^{\circ}\small.\)
Өйткені \(\displaystyle \angle ABH=\angle BAH\small,\) онда үшбұрыш \(\displaystyle ABH\) тең қабырғалы, \(\displaystyle AH=BH\small.\)
Алынған \(\displaystyle AH=BH=8\small.\)
Содан кейін \(\displaystyle KD=AD-AH-HK=17-8-3=6\small.\)
\(\displaystyle DCK\small\) тікбұрышты үшбұрышты қарастырайық Біз \(\displaystyle CK=8\) және \(\displaystyle DK=6\small\) білеміз Пифагор теоремасы бойынша \(\displaystyle CD^2=CK^2+DK^2=\) \(\displaystyle =8^2+6^2=64+36=100=10^2\small.\) \(\displaystyle CD=10\small\) Қиманың ұзындығы оң болғандықтан | 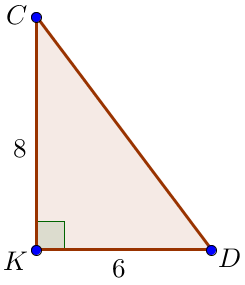 |
Жауабы: \(\displaystyle 10 \small.\)