Табандары \(\displaystyle AD\) және \(\displaystyle BC\) болатын тең қабырғалы \(\displaystyle ABCD\) трапецияда \(\displaystyle O\) диагональдардың қиылысу нүктесі, \(\displaystyle BD=12\small,\) \(\displaystyle OC=5\small,\) \(\displaystyle \angle CAD=30^\circ\small.\) \(\displaystyle O\) нүктесінен \(\displaystyle AD\small\) түзу сызыққа дейінгі қашықтықты табыңыз.
Тең қабырғалы трапеция қасиетін қолданамыз.
Тең қабырғалы трапецияның қасиеті
Тең қабырғалы трапецияның диагональдары тең.
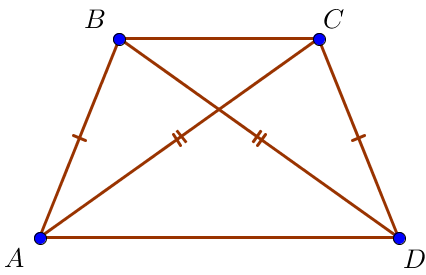
\(\displaystyle AC=BD\)
Демек,
\(\displaystyle AC=BD=12\small,\)
\(\displaystyle AO=AC-OC=12-5=7\small.\)
\(\displaystyle O\) нүктесінен \(\displaystyle AD\small\) -ға түсірілген перпендикулярдың табаны \(\displaystyle H\) болсын. \(\displaystyle OH\) кесіндінің ұзындығы \(\displaystyle О\) нүктесінен \(\displaystyle AD \) түзуіне дейінгі қашықтыққа тең. \(\displaystyle AOH\small\) тікбұрышты үшбұрышты қарастырайық Тікбұрышты үшбұрышта бұрышқа қарама-қарсы катет \(\displaystyle 30^{\circ}\small,\) гипотенузаның жартысына тең. Содан кейін \(\displaystyle OH=\frac{1}{2}\cdot {AO}=\frac{1}{2}\cdot 7=3{,}5\small.\)
| 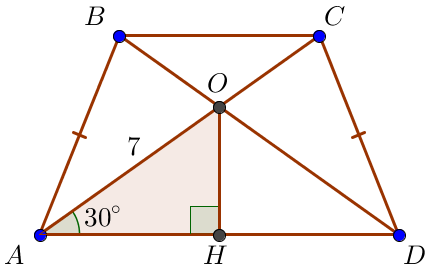 |
Жауабы: \(\displaystyle 3{,}5 {\small .}\)