Жазықтықтағы осы түзудің берілген орны бойынша түзудің дұрыс теңдеуін таңдаңыз:
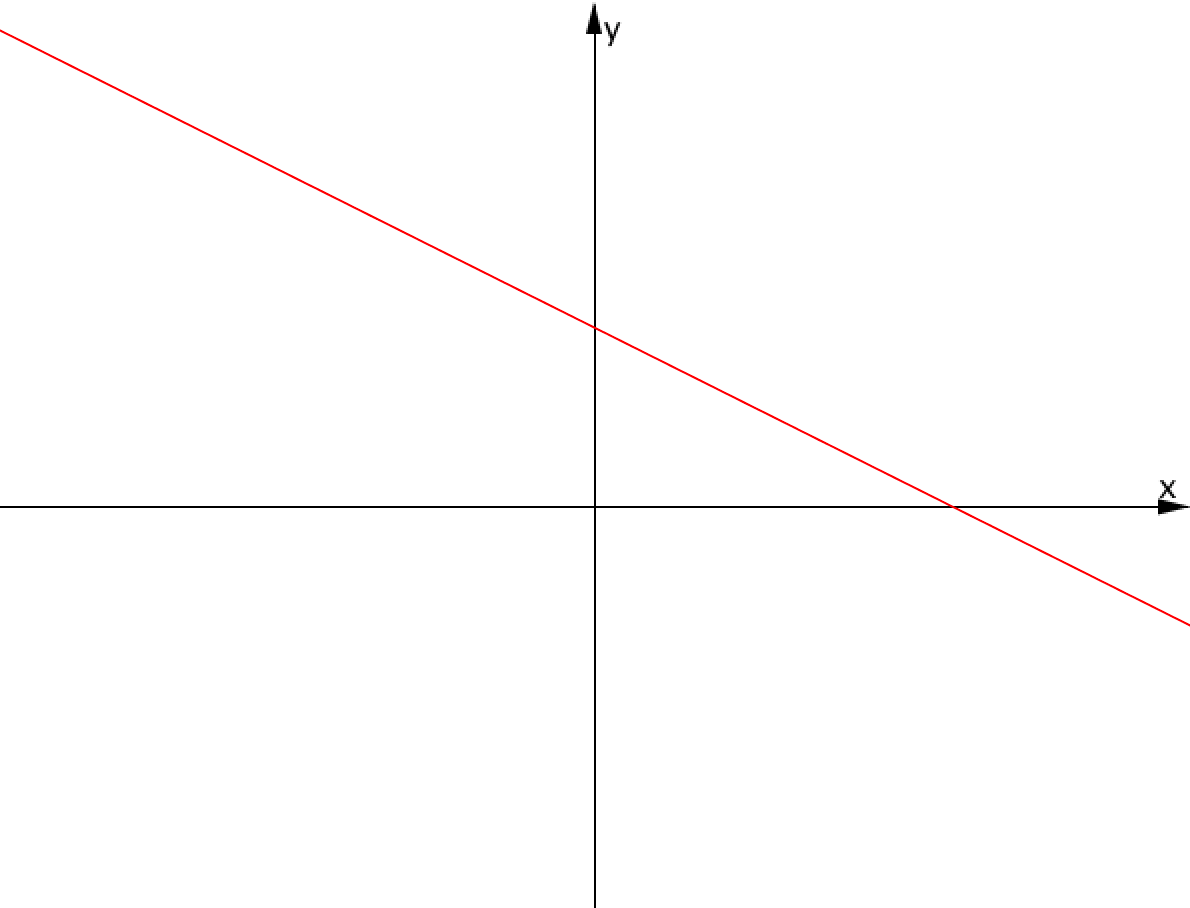
Берілген \(\displaystyle y=kx+b \) түзуі \(\displaystyle y=kx\,{\small } \) түзуін \(\displaystyle b \) бірлікке жоғары жылжыту арқылы алынған:
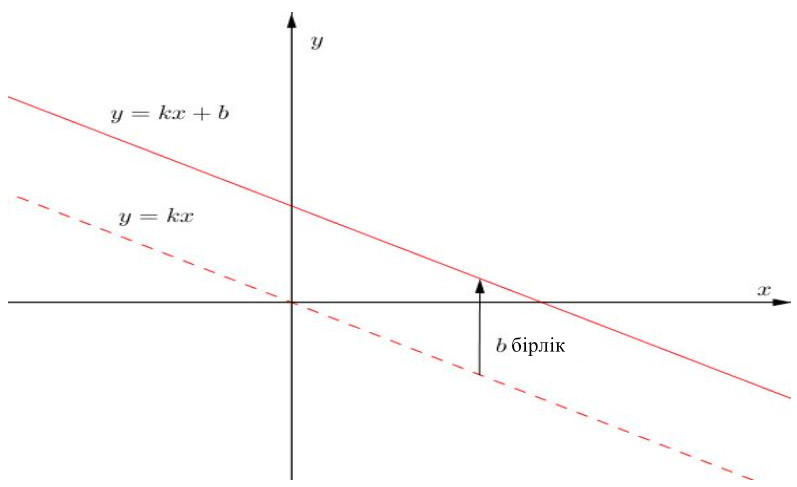
Демек, \(\displaystyle {\bf b>0}{\small .}\)
\(\displaystyle y=kx \) түзуі \(\displaystyle \rm II \) және \(\displaystyle \rm IV \) координаталық ширектерде орналасқан:
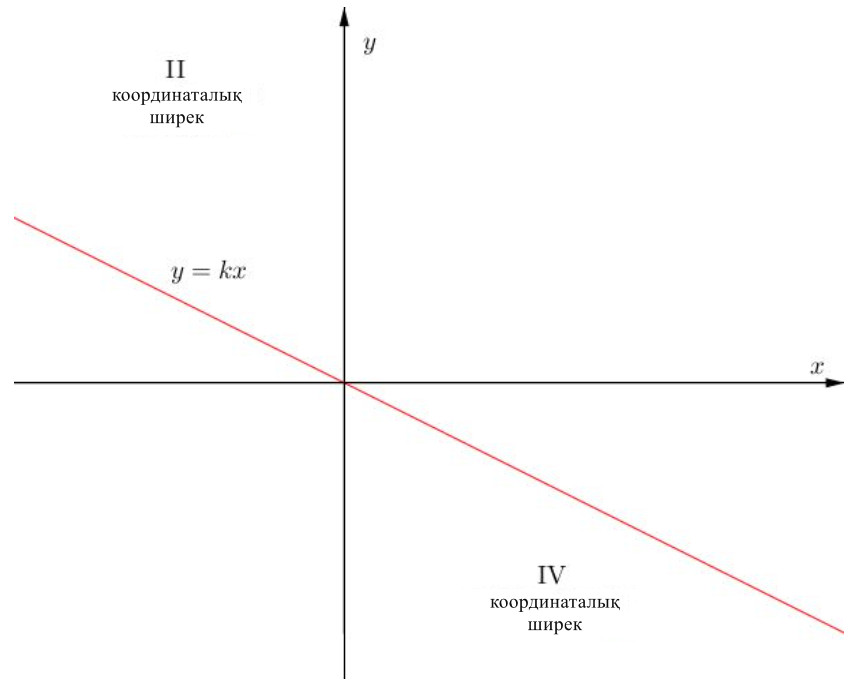
Демек, \(\displaystyle {\bf k<0} {\small .}\)
Сондықтан \(\displaystyle y=kx+b \) теңдеуінде \(\displaystyle k \) және \(\displaystyle b \) коэффициенттерінің қажетті түзу белгілері болуы керек:
\(\displaystyle k<0 \) және \(\displaystyle b>0{\small . } \)
Енді жауап нұсқаларында берілген теңдеулердегі коэффициенттердің таңбаларын анықтайық:
| Түзу \(\displaystyle y=kx+b \) | \(\displaystyle k\) | \(\displaystyle b\) | Нәтиже |
| \(\displaystyle y=\frac{2}{3}x-\frac{1}{9}\) | \(\displaystyle k=\frac{2}{3}>0 \) | \(\displaystyle b=-\frac{1}{9}<0 \) | сәйкес келмейді |
| \(\displaystyle y=-\frac{1}{2}x+3 \) | \(\displaystyle k=\color{blue}{ -\frac{1}{2}<0} \) | \(\displaystyle b=\color{blue}{ 3>0}\) | сәйкес келеді |
| \(\displaystyle y=-\frac{3}{4}x-\frac{1}{2}\) | \(\displaystyle k=-\frac{3}{4}<0\) | \(\displaystyle b=-\frac{1}{2}<0\) | сәйкес келмейді |
| \(\displaystyle y=1\frac{1}{3}x+\frac{1}{4}\) | \(\displaystyle k=1\frac{1}{3}>0\) | \(\displaystyle b=\frac{1}{4}>0\) | сәйкес келмейді |
Жауабы: \(\displaystyle y=\frac{2}{3}x-\frac{1}{9}{\small . }\)