\(\displaystyle y=kx+b\) түзуінің жазықтықтағы орны белгілі:
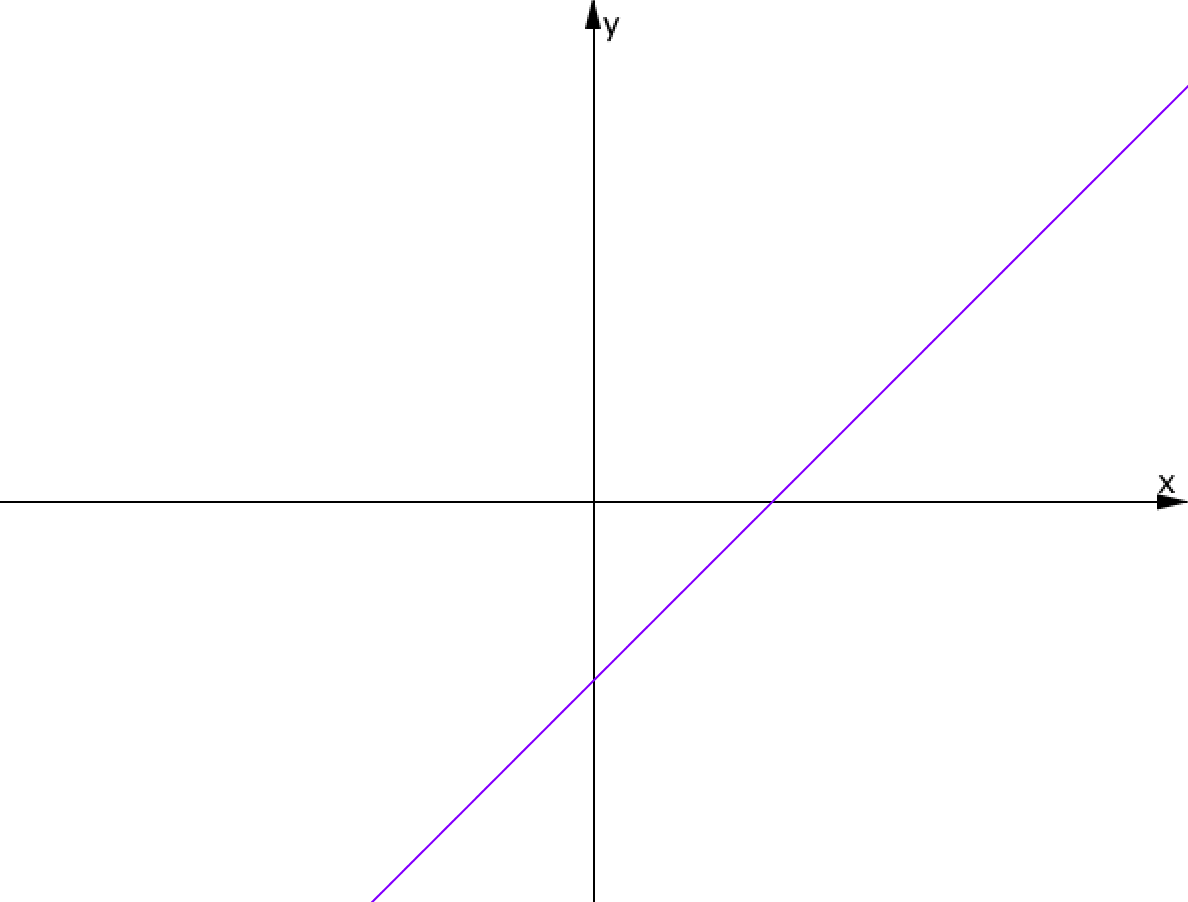
\(\displaystyle k\) және \(\displaystyle b\,{\small }\) коэффициенттерінің белгілерін анықтаңыз:
\(\displaystyle k\) \(\displaystyle 0\)
\(\displaystyle b\) \(\displaystyle 0\)
Егер \(\displaystyle b{\small }\) коэффициентін алып тастаса, онда \(\displaystyle y=kx+b \) бастапқы сызығына параллель және координаттардың басынан өтетін \(\displaystyle y=kx{\small } \) түзуі алынады. . Басқаша айтқанда, \(\displaystyle y=kx+b \) түзуі \(\displaystyle y=kx{\small } \) түзуінен \(\displaystyle b \) бірлікке төмен жылжыту арқылы алынған:
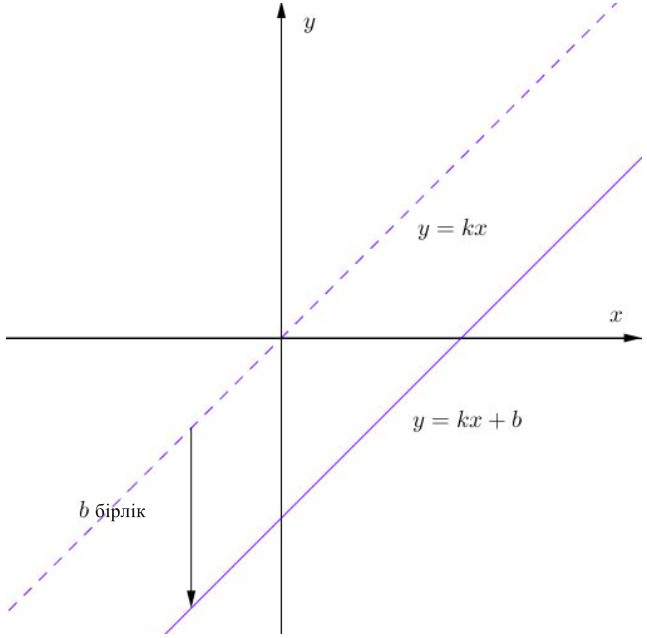
Яғни, \(\displaystyle \bf b<0{\small . } \)
\(\displaystyle y=kx \) түзуі \(\displaystyle \rm I \) және \(\displaystyle \rm III \) координаталық ширектерде жатыр:
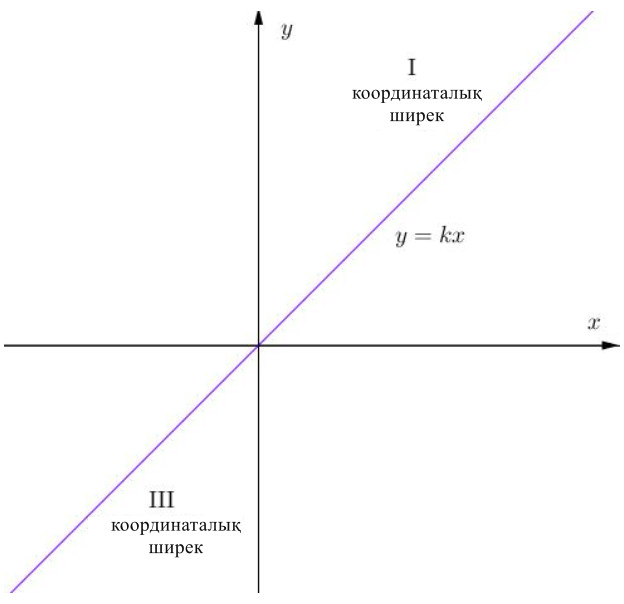
Сондықтан оның коэффициенті \(\displaystyle \bf k>0{\small . } \)
Осылайша, \(\displaystyle \bf k>0 \) және \(\displaystyle \bf b<0{\small . } \)