Суретте екі түзу көрсетілген:
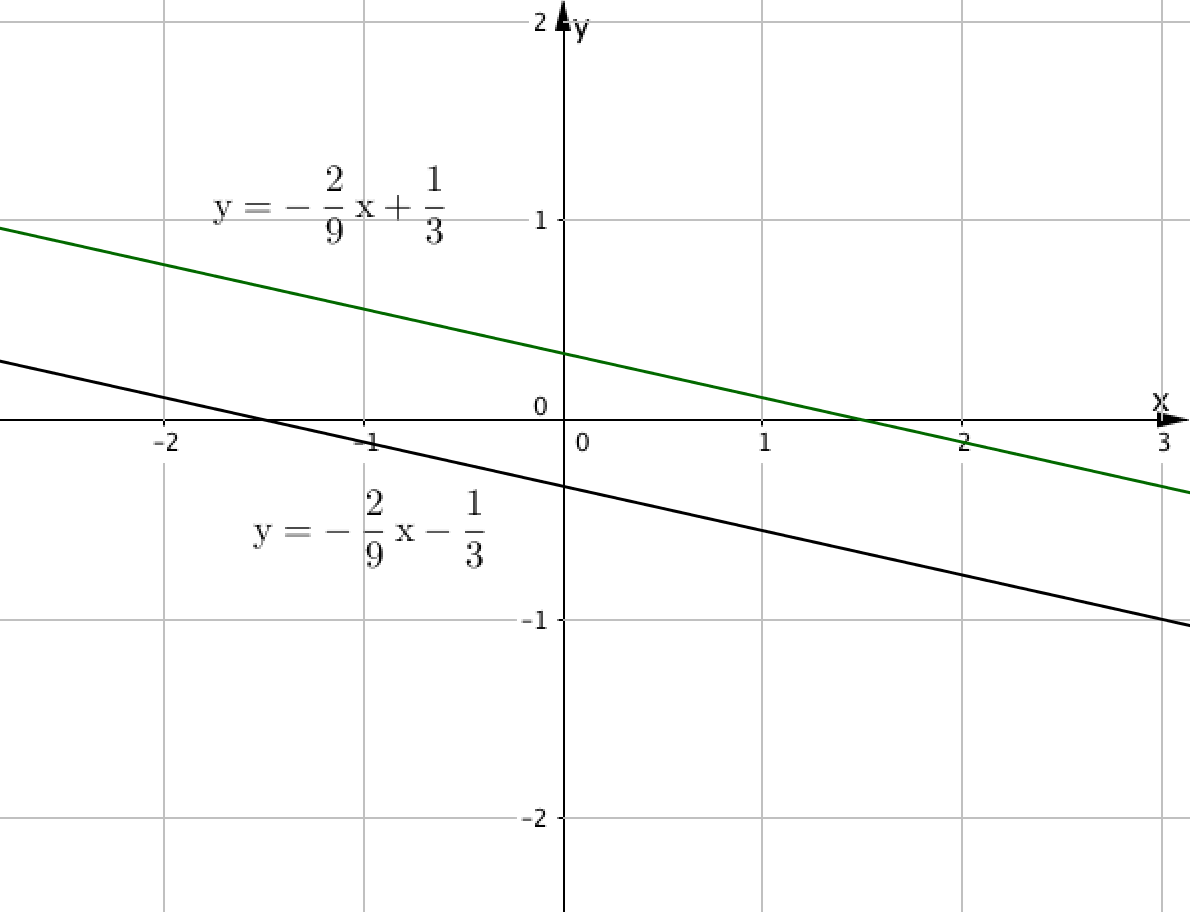
Бізге берілген теңдеулерді бірінің үстіне бірін жазайық:
| \(\displaystyle y=\color{blue}{ -\frac{2}{9}x}-\color{green}{ \frac{1}{3}}{\small , }\) |
| \(\displaystyle y=\color{blue}{ -\frac{2}{9}x}+\color{green}{ \frac{1}{3}}{\small . }\) |
Бұл жазбадан \(\displaystyle y=\color{blue}{ -\frac{2}{9}x}+\color{green}{ \frac{1}{3}}\) теңдеуі \(\displaystyle y=\color{blue}{ -\frac{2}{9}x}-\color{green}{ \frac{1}{3}}\) теңдеуінен \(\displaystyle \color{green}{ \frac{1}{3}}-\left(-\color{green}{ \frac{1}{3}}\right)=\color{green}{ \frac{2}{3}}{\small } \) қосу арқылы алынғанын көруге болады.
Егер \(\displaystyle y=f(x) \) функциясының графигін \(\displaystyle \color{blue}{\rm A} \) бірліктеріне жоғары көтерсеңіз, \(\displaystyle y=f(x)+\color{blue}{\rm A}{\small } \) функциясының графигі алынады.
Ережеге сәйкес, бұл \(\displaystyle y=-\frac{2}{9}x+\frac{1}{3}\) түзуі \(\displaystyle y=-\frac{2}{9}x-\frac{1}{3}\) түзуінен \(\displaystyle \bf \frac{2}{3}\) бірлікке жоғары жылжыту арқылы алынғанын білдіреді.