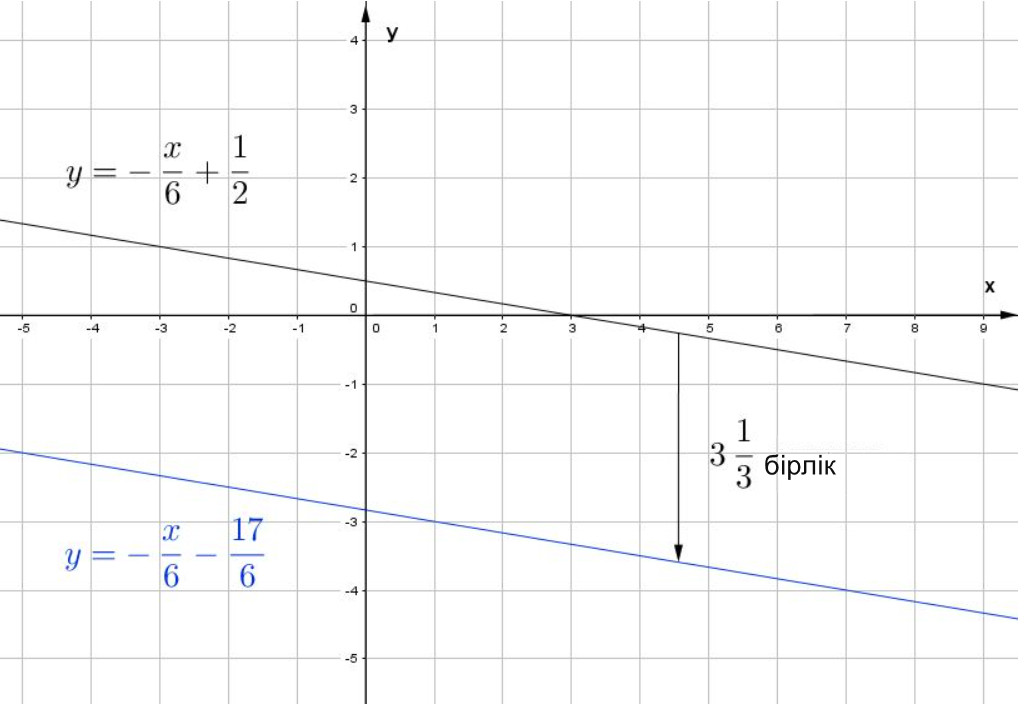
\(\displaystyle y=-\frac{x}{6}+\frac{1}{2}\) түзуін \(\displaystyle 3\frac{1}{3}\) бірлікке төмен жылжыту арқылы алынған түзудің теңдеуін жазыңыз (\(\displaystyle \rm OY\) осі бойымен).
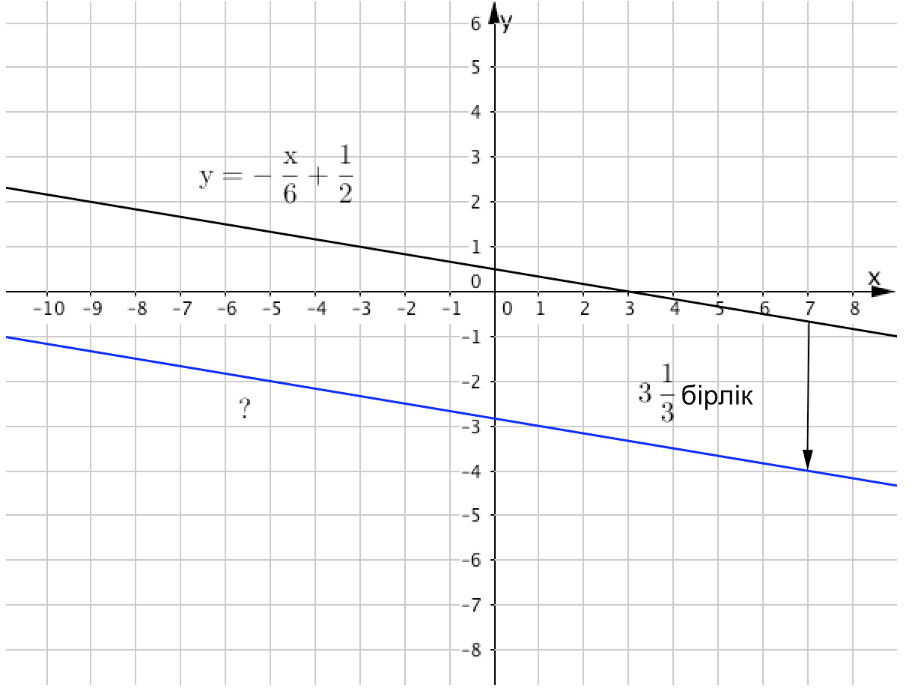
Егер \(\displaystyle y=f(x) \) функциясының графигін \(\displaystyle \color{blue}{\rm A} \) бірлікке төмен түсірсе, \(\displaystyle y=f(x)-\color{blue}{\rm A}{\small } \) функциясының графигі алынады.
Бізге \(\displaystyle y=\color{green}{ -\frac{x}{6}+\frac{1}{2}}{\small } \) функциясының графигі берілген және біз оны \(\displaystyle \color{blue}{ 3\frac{1}{3}}\) бірлікке төмендетеміз.
Сонда ережеге сәйкес бізде келесідей функция графигі болады:
\(\displaystyle y=\left(\color{green}{ -\frac{x}{6}+\frac{1}{2}}\right)-\color{blue}{ 3\frac{1}{3}}=-\frac{x}{6}+\frac{1}{2}-\frac{10}{3}=-\frac{x}{6}-\frac{17}{6}{\small . } \)