Суретте екі түзу көрсетілген:
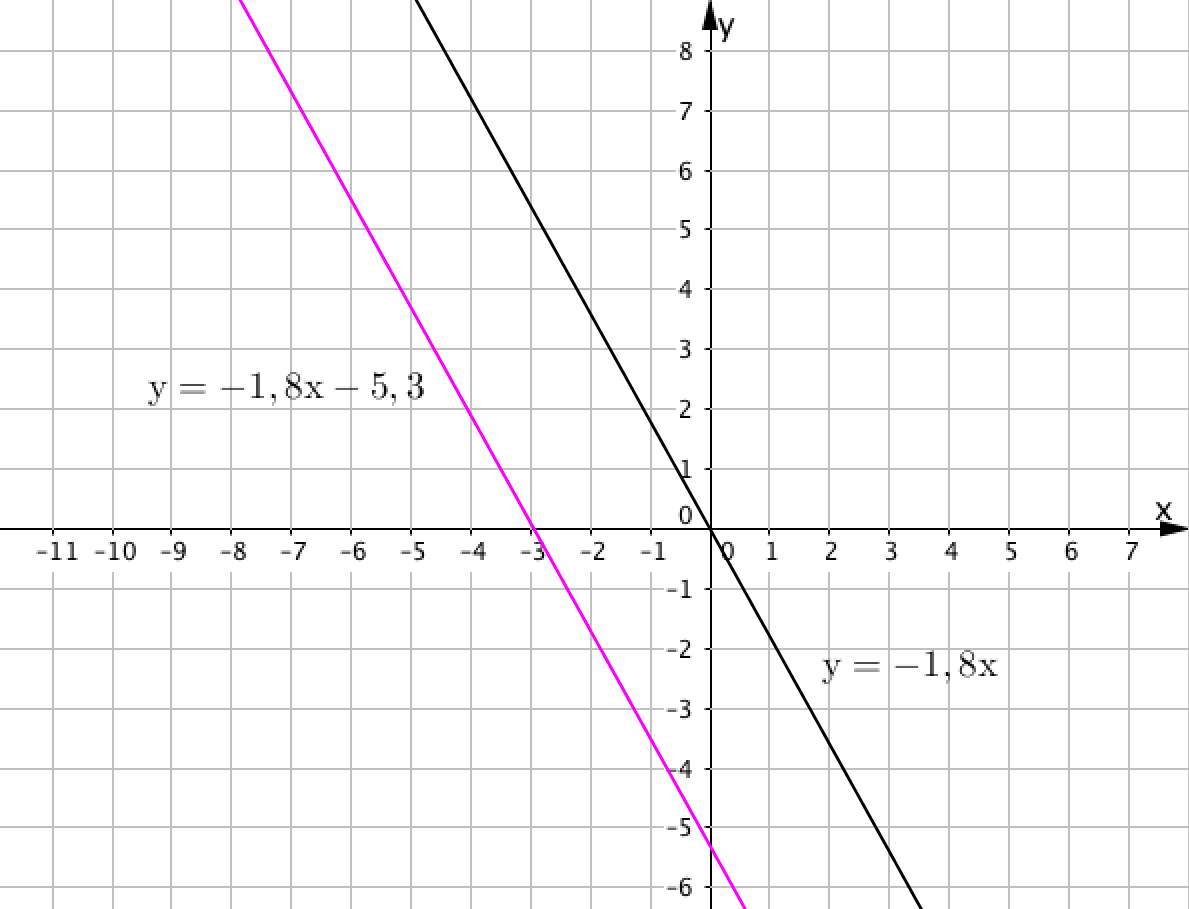
Егер \(\displaystyle y=f(x) \) функциясының графигін \(\displaystyle \color{blue}{\rm A} \) бірлікке төммен түсірсе, \(\displaystyle y=f(x)-\color{blue}{\rm A}{\small } \) функциясының графигі алынады
Ыңғайлы болу үшін берілген теңдеулерді бірінің үстіне бірін жазайық:
| \(\displaystyle y=\color{blue}{ -1{,}8x}-5{,}3{\small ; }\) |
| \(\displaystyle y=\color{blue}{ -1{,}8x}{\small . }\) |
Жазылғаннан \(\displaystyle y=\color{blue}{ -1{,}8x}-5{,}3\) теңдеуі \(\displaystyle y=\color{blue}{ -1{,}8x}\) теңдеуінен \(\displaystyle 5{,}3{\small } \) азайту арқылы алынғанын көруге болады.
Жоғарыда келтірілген ережеге сәйкес, бұл \(\displaystyle y=-1{,}8x-5{,}3\) түзуі \(\displaystyle y=-1{,}8x \) түзуінен \(\displaystyle 5{,}3{\small } \) бірлікке төмен жылжу арқылы алынғанын білдіреді.