Изменяя угол \(\displaystyle t\) и перемещая точку \(\displaystyle A\) по единичной окружности, найдите приближенное значение косинуса.
\(\displaystyle \cos(5{,}3)\approx \)

Дана единичная окружность с центром в точке \(\displaystyle O{\small.}\) Точка \(\displaystyle A\) имеет координаты \(\displaystyle (1;0){\small .}\)
Луч \(\displaystyle OA\) повернулся на угол \(\displaystyle \color{red}{\alpha}{\small.}\)
Тогда
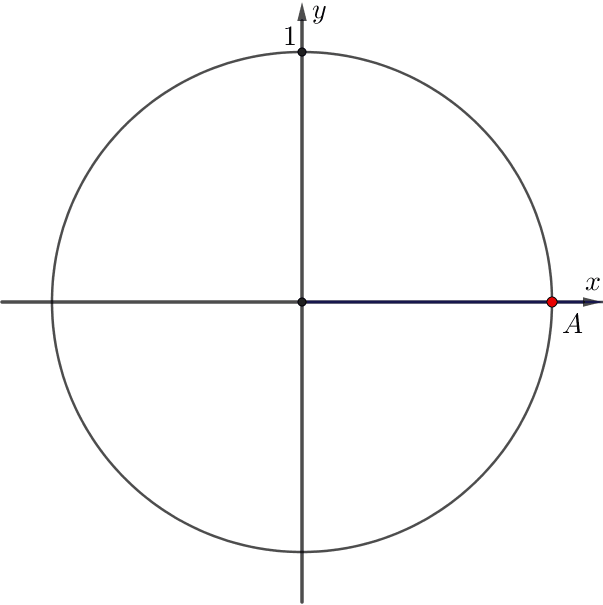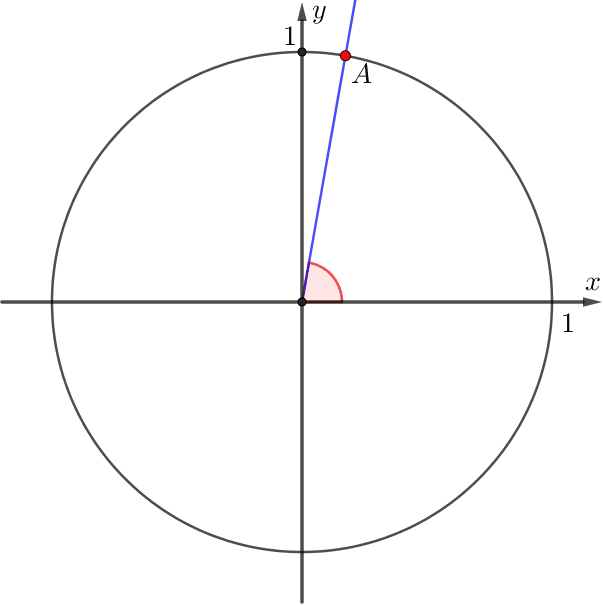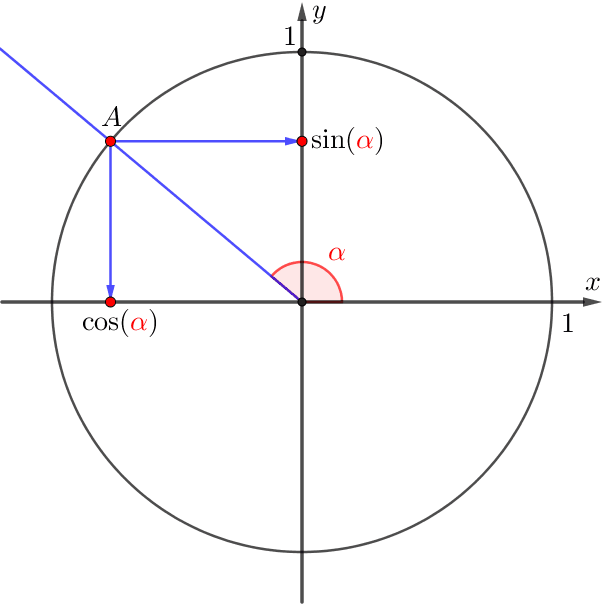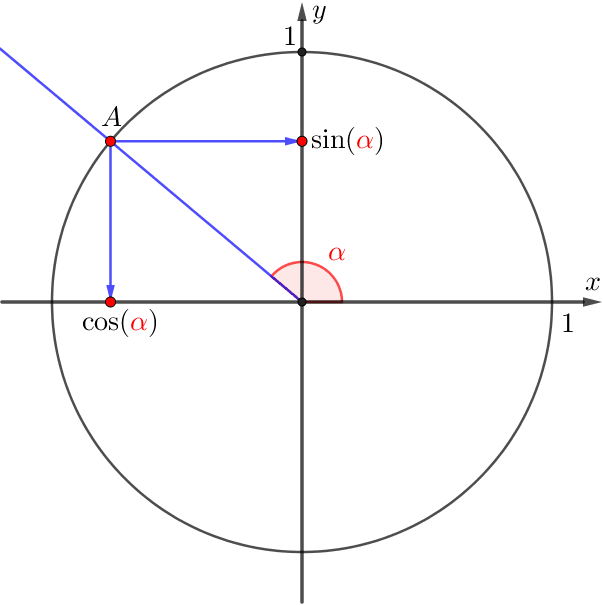
- косинусом угла \(\displaystyle \color{red}{\alpha}\) называется абсцисса точки \(\displaystyle A\) и обозначается \(\displaystyle \cos(\color{red}{\alpha}){\small,}\)
- синусом угла \(\displaystyle \color{red}{\alpha}\) называется ордината точки \(\displaystyle A\) и обозначается \(\displaystyle \sin(\color{red}{\alpha}){\small.}\)
Перемещая параметр \(\displaystyle t\) на значение \(\displaystyle t=5{,}3{ \small ,}\) получаем точку \(\displaystyle A=(\cos(5{,}3);\, \sin(5{,}3)){\small .}\)

На графике показано, что координата точки \(\displaystyle A\) по оси \(\displaystyle \rm OX\) имеет значение \(\displaystyle x_A=0{,}554{\small .}\)
Таким образом,
\(\displaystyle \cos(5{,}3)\approx 0{,}554{\small .}\)