Найдите \(\displaystyle \sqrt{10}\cos\alpha,\) если \(\displaystyle \tg \alpha = \frac{1}{3} \) и \(\displaystyle \alpha \in \left(\pi; \frac{3\pi}{2} \right){\small.}\)
\(\displaystyle \sqrt{10}\cos\alpha=\)
Применим формулу
\(\displaystyle \tg\alpha=\frac{\sin\alpha}{\cos\alpha}\)
По условию \(\displaystyle \tg \alpha = \frac{1}{3},\) то есть
\(\displaystyle \frac{\sin\alpha}{\cos\alpha}=\frac{1}{3}{\small .}\)
Так как требуется найти \(\displaystyle \cos\alpha{ \small ,} \) то выразим \(\displaystyle \sin\alpha{\small : } \)
\(\displaystyle \sin\alpha=\frac{1 \cdot \cos \alpha}{3},\)
\(\displaystyle \sin\alpha=\frac{1}{3}\cos \alpha{\small .}\)
Подставим полученное выражение вместо \(\displaystyle \sin\alpha\) в основное тригонометрическое тождество:
\(\displaystyle \sin^2\alpha+\cos^2\alpha=1\),
\(\displaystyle \bigg(\frac{1}{3}\cos \alpha \bigg)^2+\cos^2\alpha=1{\small .}\)
Найдем \(\displaystyle \cos\alpha{:}\)
\(\displaystyle \frac{1}{9}\cos^2 \alpha +\cos^2\alpha=1,\)
\(\displaystyle \frac{10}{9}\cos^2 \alpha =1,\)
\(\displaystyle \cos^2 \alpha =\frac{9}{10},\)
\(\displaystyle \cos \alpha =\pm \sqrt{\frac{9}{10}},\)
\(\displaystyle \cos\alpha=\pm \frac{3}{\sqrt{10}}{\small.}\)
Определим, какой именно знак имеет \(\displaystyle \cos\alpha\) по заданному интервалу для угла \(\displaystyle \alpha{\small.}\)
По условию \(\displaystyle \alpha \in \left(\pi; \frac{3\pi}{2} \right){\small.}\)
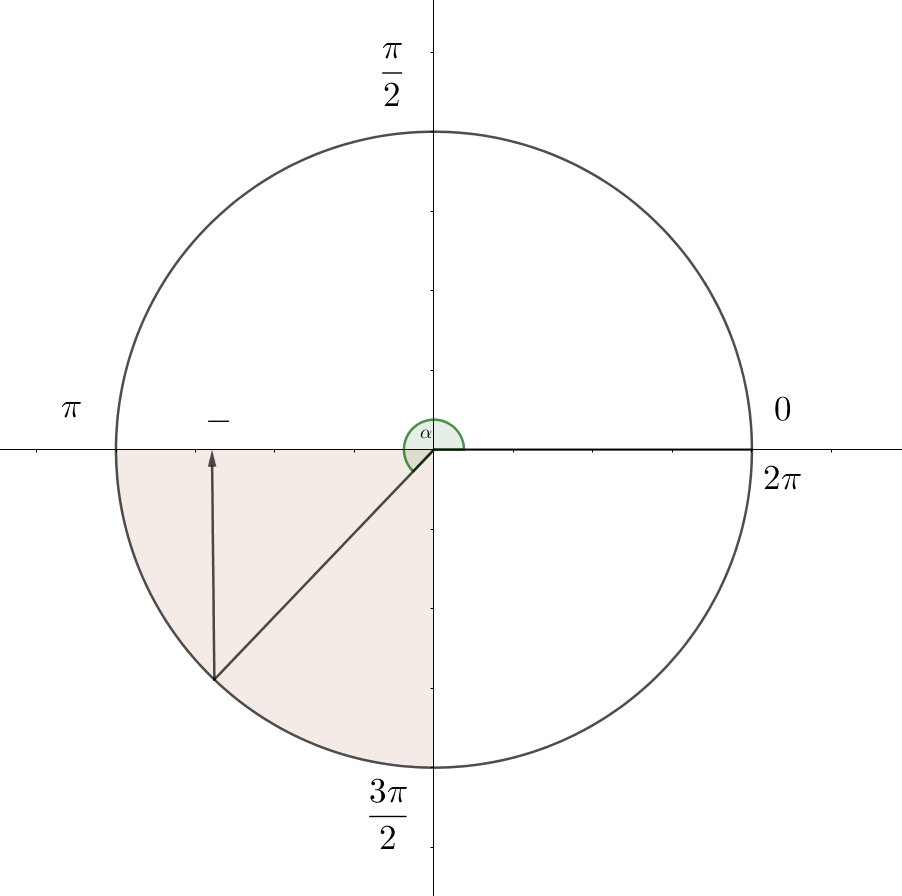
В третьей четверти значение косинуса отрицательно. Следовательно,
\(\displaystyle \cos\alpha=-\frac{3}{\sqrt{10}}{\small.}\)
Тогда
\(\displaystyle \sqrt{10}\cos\alpha =\sqrt{10}\cdot \bigg(-\frac{3}{\sqrt{10}} \bigg )=-3{\small.}\)
Ответ:\(\displaystyle -3{\small.}\)