Задание
Дан график функции \(\displaystyle y=\frac{5}{x}{\small .}\)
Двигая ползунки \(\displaystyle a\) и \(\displaystyle b{ \small ,}\) постройте график функции \(\displaystyle y=\frac{5}{x+1}+1{,}5{\small .}\)
Параметры \(\displaystyle a\) и \(\displaystyle b{\small .}\)
Запишите полученное значение:
\(\displaystyle \color{green}{A}=\)
.
Решение
Требуется получить из гиперболы \(\displaystyle y=\frac{5}{x}\) график функции \(\displaystyle y=\frac{5}{x+1}+1{,}5{\small .}\)
Получим из гиперболы \(\displaystyle y=\frac{5}{x}\) график функции \(\displaystyle y=\frac{5}{x+1}{\small ,}\) применив правило.
Правило
- Если график функции \(\displaystyle y=f(x) \) сдвинуть на \(\displaystyle \color{blue}{\rm A} \) единиц вправо, получится график функции \(\displaystyle y=f(x{\bf-}\color{blue}{\rm A}){\small . } \)
- Если график функции \(\displaystyle y=f(x) \) сдвинуть на \(\displaystyle \color{blue}{\rm A} \) единиц влево, получится график функции \(\displaystyle y=f(x{\bf+}\color{blue}{\rm A}){\small . } \)
Получаем сдвиг на \(\displaystyle 1\) единицу влево:
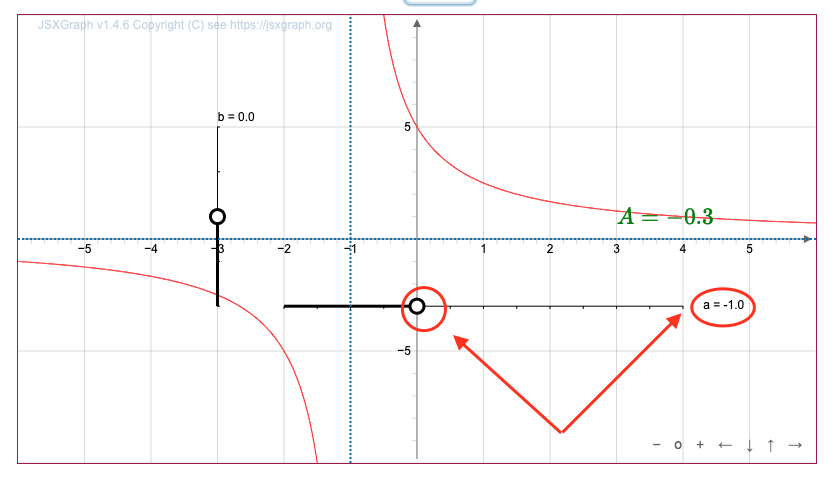
Получим из графика функции \(\displaystyle y=\frac{5}{x+1}\) график функции \(\displaystyle y=\frac{5}{x+1}+1{,}5{\small ,}\) применив правило.
Правило
- Если график функции \(\displaystyle y=f(x) \) сдвинуть на \(\displaystyle \color{blue}{\rm A} \) единиц вверх, получится график функции \(\displaystyle y=f(x){\bf+}\color{blue}{\rm A}{\small . } \)
- Если график функции \(\displaystyle y=f(x) \) сдвинуть на \(\displaystyle \color{blue}{\rm A} \) единиц вниз, получится график функции \(\displaystyle y=f(x){\bf-}\color{blue}{\rm A}{\small . } \)
Получаем сдвиг на \(\displaystyle 1{,}5\) единицы вверх:

Тогда параметр \(\displaystyle \color{green}{A}\) имеет значение \(\displaystyle 1{,}2{\small .}\)

Ответ:\(\displaystyle \color{green}{A}=1{,}2{\small .}\)