Запишите уравнение параболы, полученной из параболы \(\displaystyle y=x^2\) её сжатием вдоль оси \(\displaystyle \rm OY\) в \(\displaystyle 8\) раз.
\(\displaystyle y=\)
Воспользуемся определением.
График функции
Графиком функции \(\displaystyle y=\color{blue}{f(x)}\) на плоскости называется множество точек
\(\displaystyle \{(x;\, \color{blue}{f(x)})| \, x\) принадлежит области определения\(\displaystyle \}{\small .}\)
Графиком параболы \(\displaystyle y=x^2\) является множество точек вида \(\displaystyle \{(x;\, x^2) \}\) для всех действительных чисел \(\displaystyle x{\small .}\)
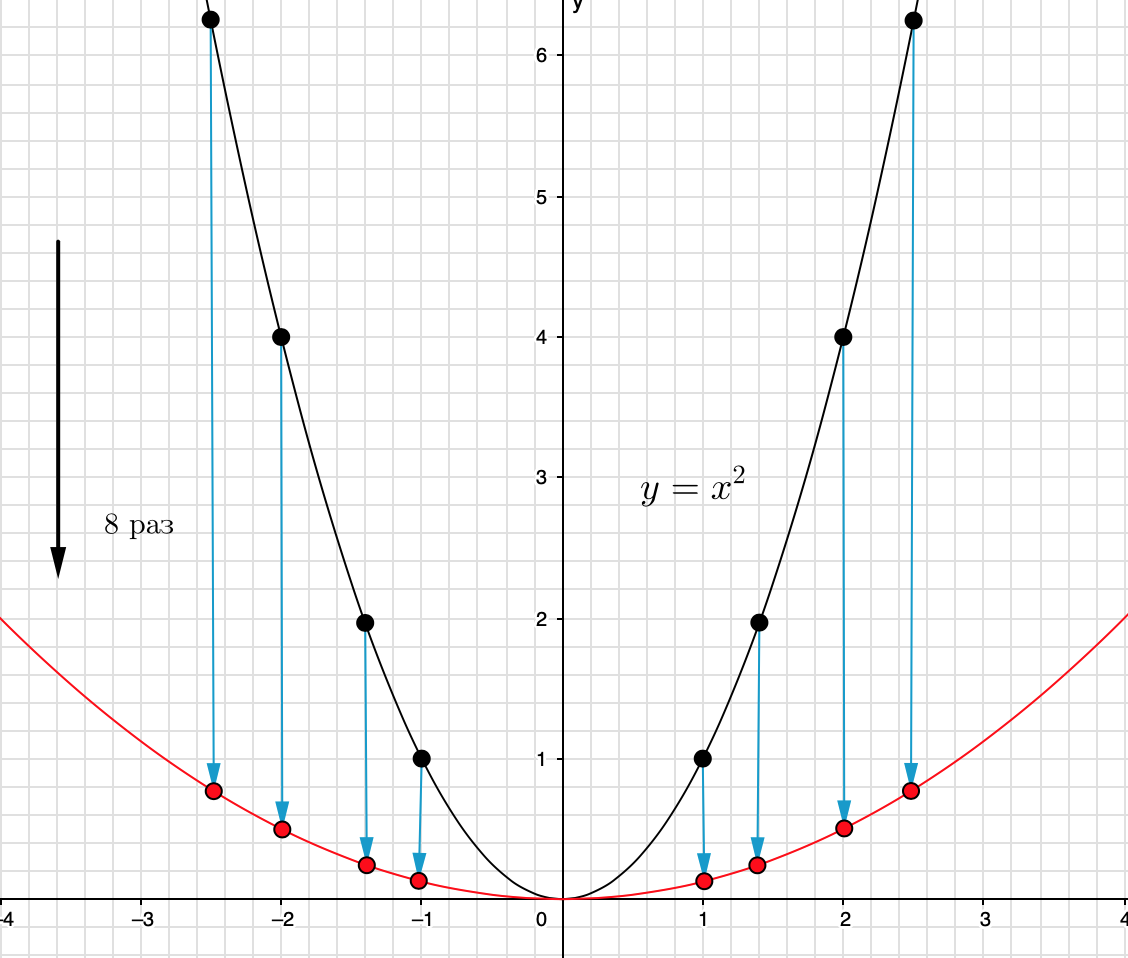
Сжать график параболы \(\displaystyle y=x^2\) вдоль оси \(\displaystyle \rm OY \) означает сжать каждую точку этого графика вдоль оси \(\displaystyle \rm OY{\small .} \)
Значит, нужно взять каждую точку из множества точек \(\displaystyle \{(x;\, x^2) \}\) и сжать ее вдоль оси \(\displaystyle \rm OY{\small .} \)
Возьмем одну точку вида \(\displaystyle (x;\, x^2)\) и сожмем ее в \(\displaystyle 8\) раз вдоль оси \(\displaystyle \rm OY{\small ,} \) то есть уменьшим значение ординаты в \(\displaystyle 8\) раз.
Если ординату этой точки \(\displaystyle (x;\, x^2)\) уменьшить в \(\displaystyle \color{blue}{8}\) раз, то это будет точка с координатами \(\displaystyle (x;\, \color{blue}{\frac{1}{8}} \cdot x^2){\small : }\)
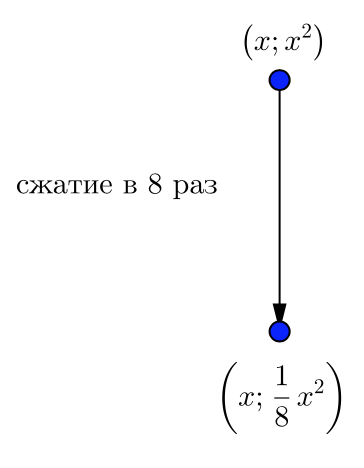
Проделывая такую же операцию с каждой точкой вида \(\displaystyle (x;\,x^2) { \small ,}\) получаем множество точек \(\displaystyle \{(x;\, \color{blue}{\frac{1}{8}}x^2) \}{ \small ,}\) что является графиком параболы \(\displaystyle y=\color{blue}{\frac{1}{8}}x^2{\small :}\)
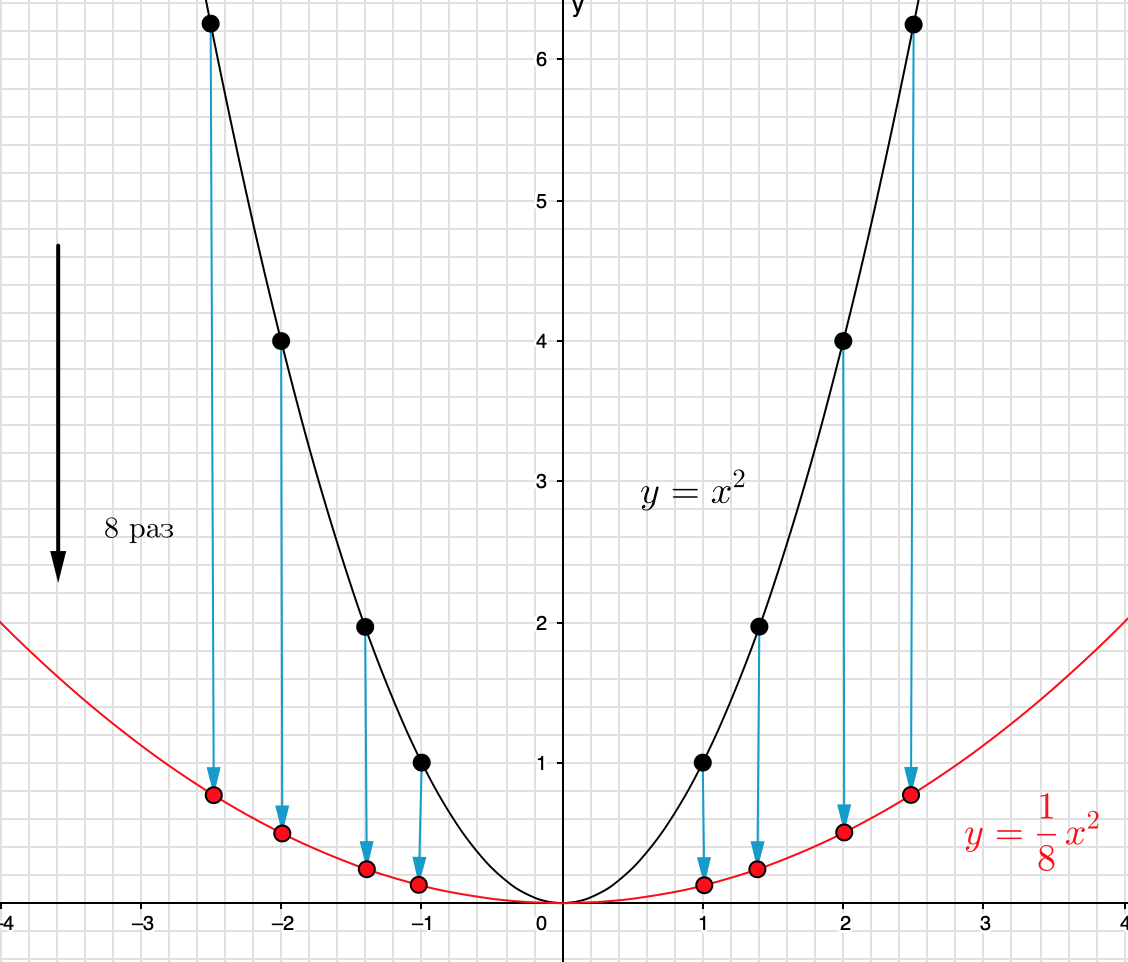
Ответ: \(\displaystyle y=\frac{1}{8}x^2{\small .}\)