Для квадратичной функции \(\displaystyle y=-2x^2\) найдите её промежутки возрастания и убывания.
Часть 1: Построение графика квадратичной функции \(\displaystyle y=-2x^2{\small .}\)
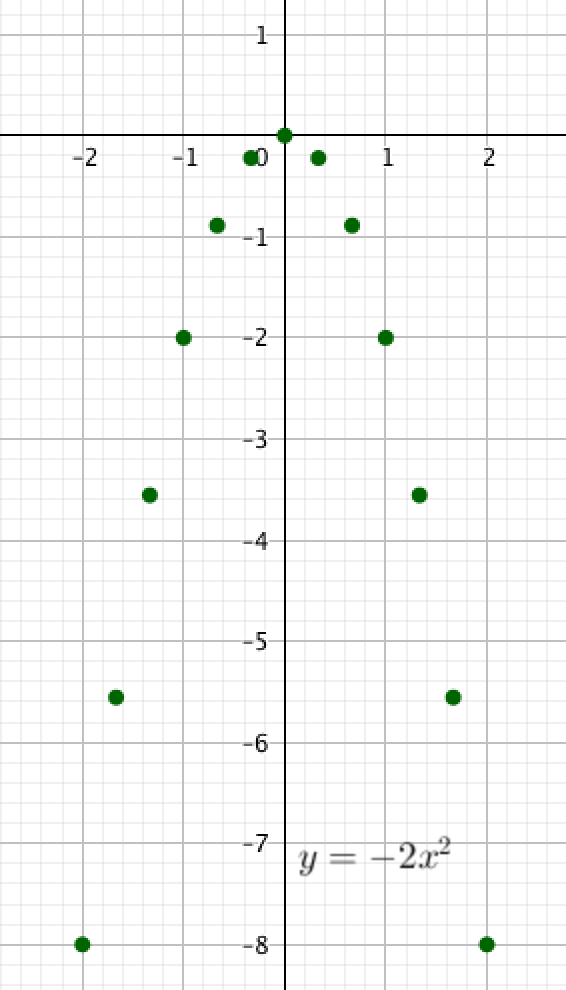
Вычислим значения квадратичной функции \(\displaystyle y=-2x^2\) в нескольких точках:
| \(\displaystyle x\) | \(\displaystyle -2\) | \(\displaystyle -1\frac{2}{3}\) | \(\displaystyle -1\frac{1}{3}\) | \(\displaystyle -1\) | \(\displaystyle -\frac{2}{3}\) | \(\displaystyle -\frac{1}{3}\) | \(\displaystyle 0\) | \(\displaystyle \frac{1}{3}\) | \(\displaystyle \frac{2}{3}\) | \(\displaystyle 1\) | \(\displaystyle 1\frac{1}{3}\) | \(\displaystyle 1\frac{2}{3}\) | \(\displaystyle 2\) |
| \(\displaystyle y=-2x^2\) | \(\displaystyle -8\) | \(\displaystyle -5\frac{5}{9}\) | \(\displaystyle -3\frac{5}{9}\) | \(\displaystyle -2\) | \(\displaystyle -\frac{8}{9}\) | \(\displaystyle -\frac{2}{9}\) | \(\displaystyle 0\) | \(\displaystyle -\frac{2}{9}\) | \(\displaystyle -\frac{8}{9}\) | \(\displaystyle -2\) | \(\displaystyle -3\frac{5}{9}\) | \(\displaystyle -5\frac{5}{9}\) | \(\displaystyle -8\) |
и построим их на числовой плоскости:
Посторим непрерывную линию по данным точкам:
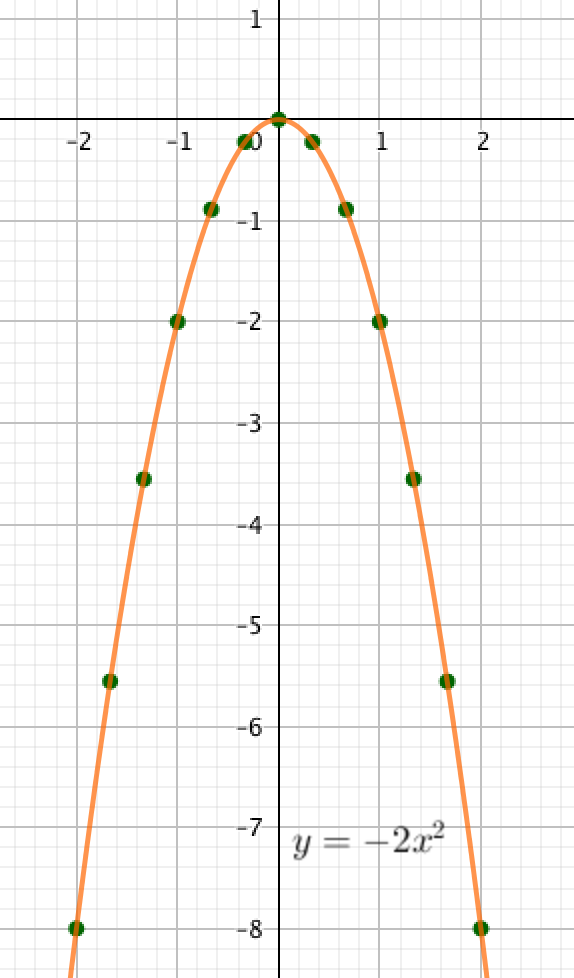
Часть 2: Убывание и возрастание.
Возрастание функции
Функция \(\displaystyle y=f(x)\) возрастает на промежутке \(\displaystyle x \in (a;\, b){\small ,}\)
- если большему значению \(\displaystyle x\) на этом промежутке соответствует большее значение функции \(\displaystyle f(x){\small ,}\)
- то есть для любых \(\displaystyle x_1{ \small ,}\, x_2 \in (a;\, b){\small ,}\) если \(\displaystyle x_2>x_1{\small ,}\) то \(\displaystyle f(x_2)>f(x_1){\small .}\)
Из графика видно, что
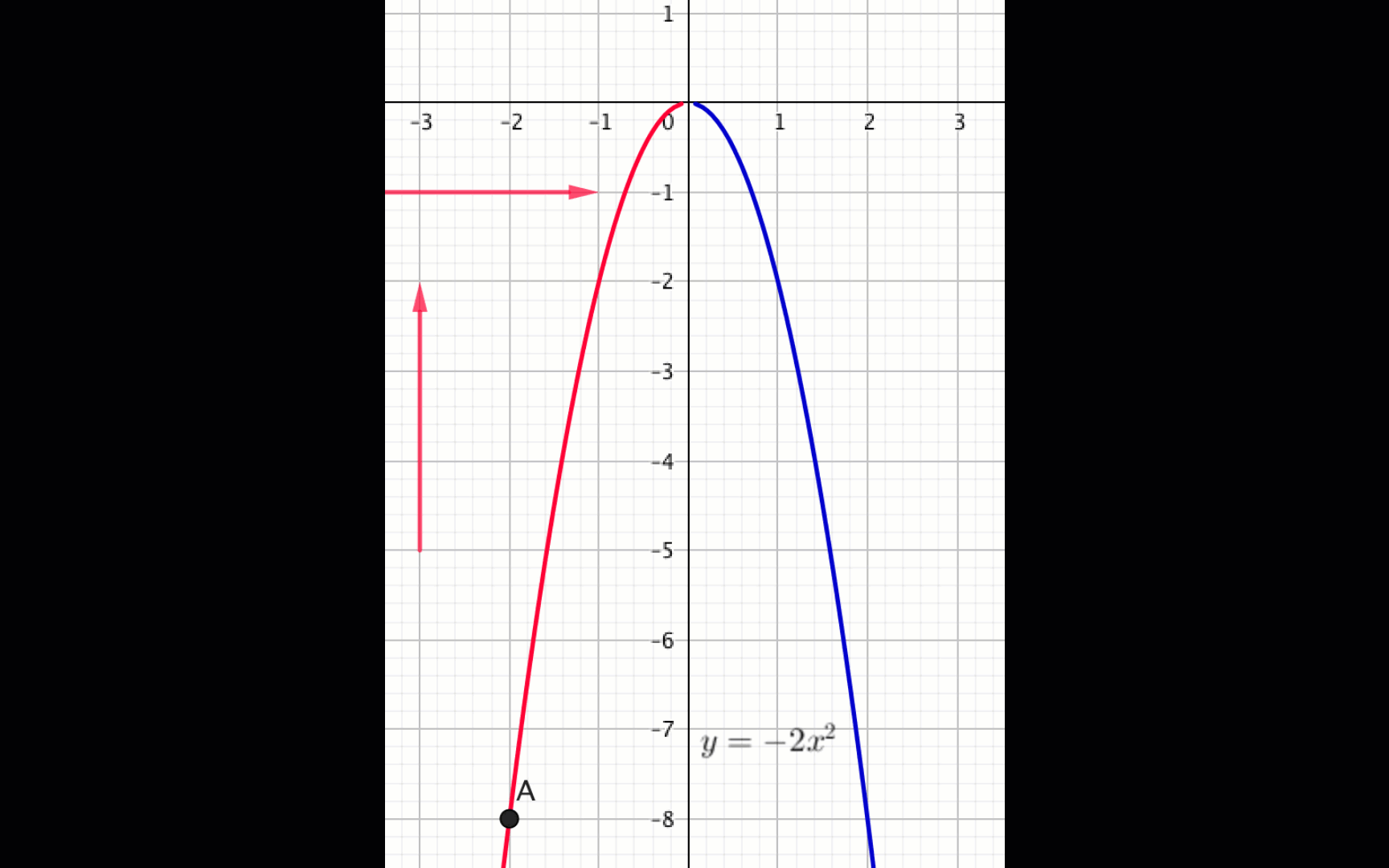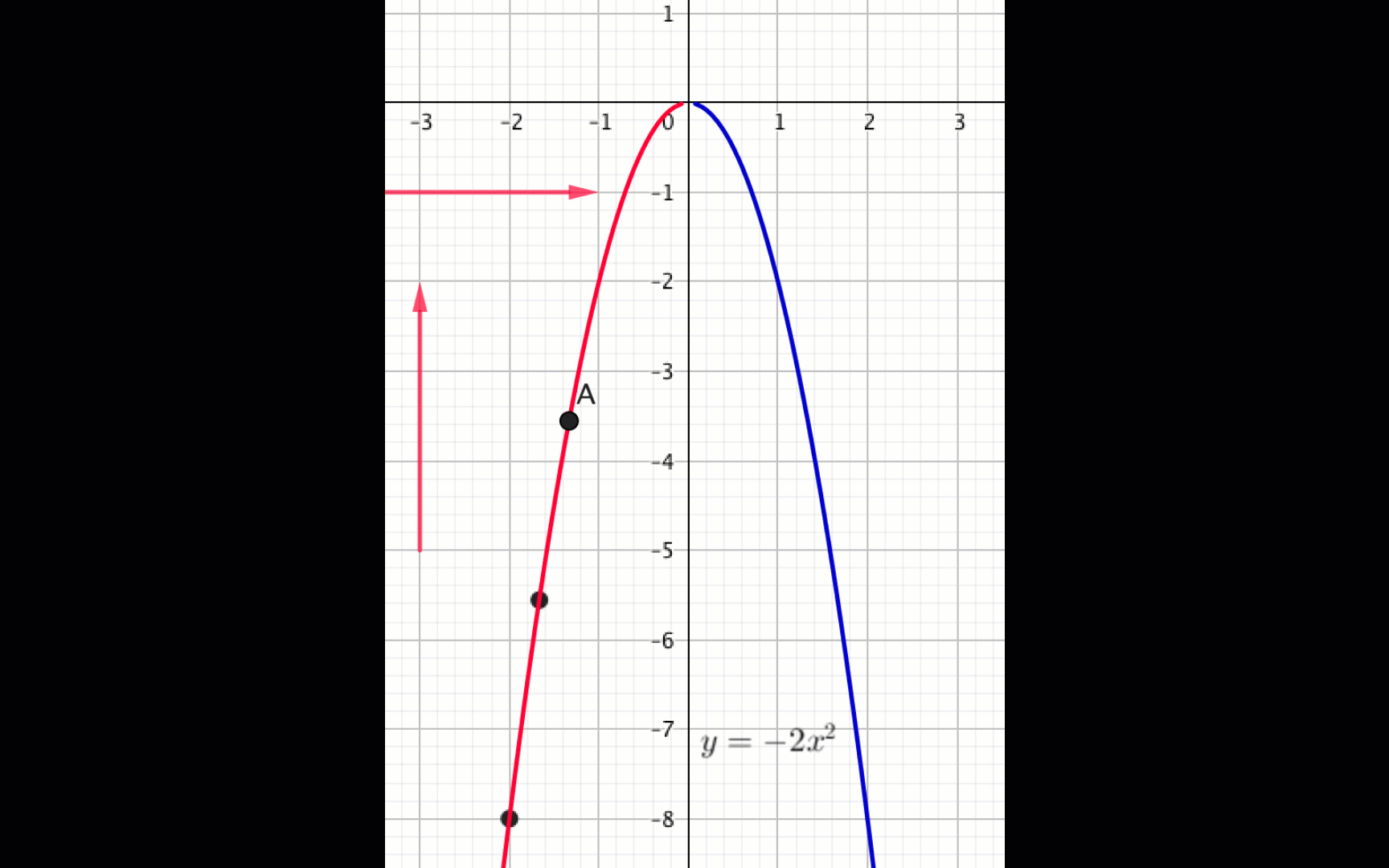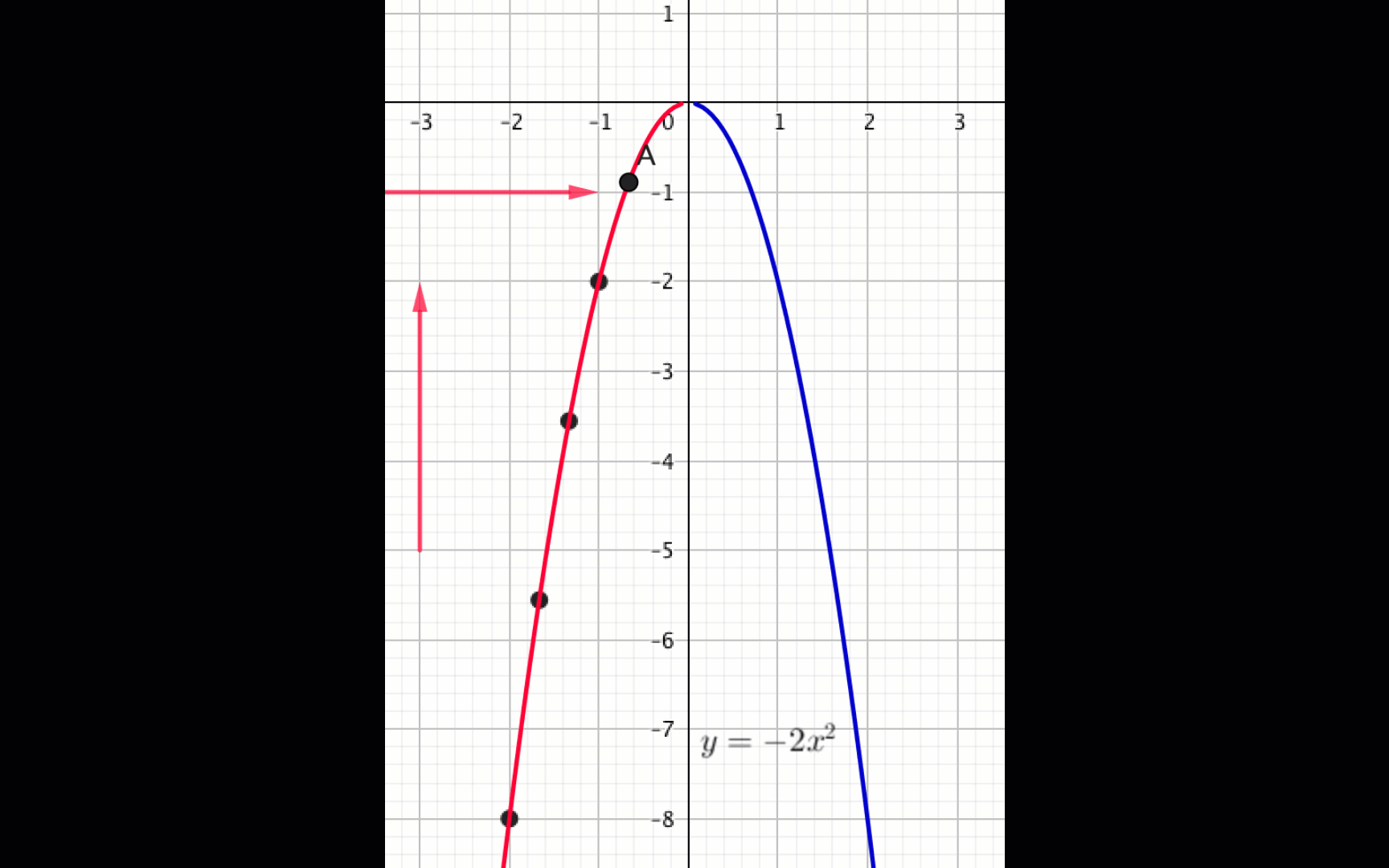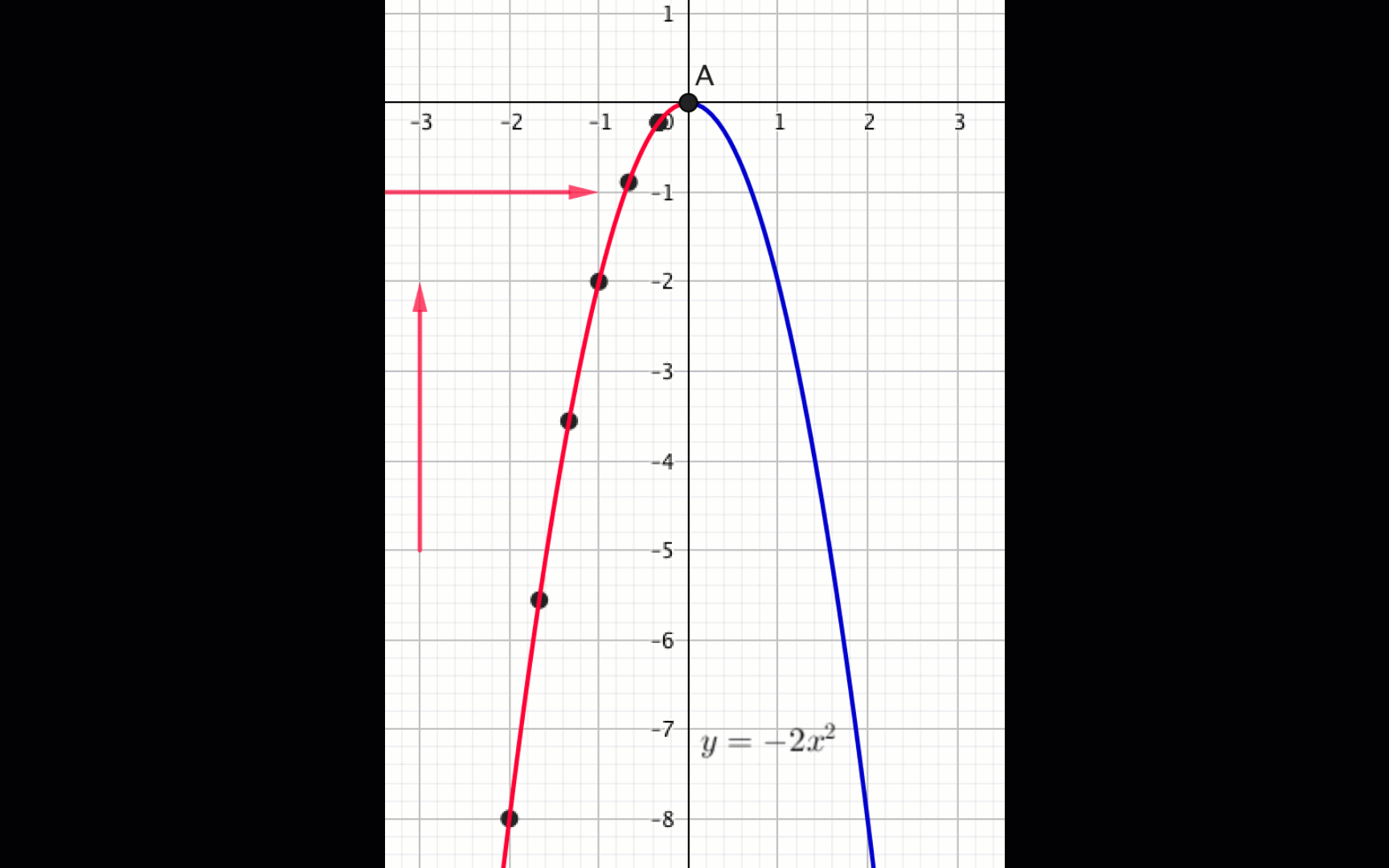
функция \(\displaystyle f(x)=-2x^2\) возрастает, если \(\displaystyle x \in (-\infty;\, 0){\small .}\)
Убывание функции
Функция \(\displaystyle y=f(x)\) убывает на промежутке \(\displaystyle x \in (a;\, b){\small ,}\)
- если большему значению \(\displaystyle x\) на этом промежутке соответствует меньшее значение функции \(\displaystyle f(x){\small ,}\)
- то есть для любых \(\displaystyle x_1{ \small ,}\, x_2 \in (a;\, b){\small ,}\) если \(\displaystyle x_2>x_1{\small ,}\) то \(\displaystyle f(x_2)<f(x_1){\small .}\)
Из графика видно, что
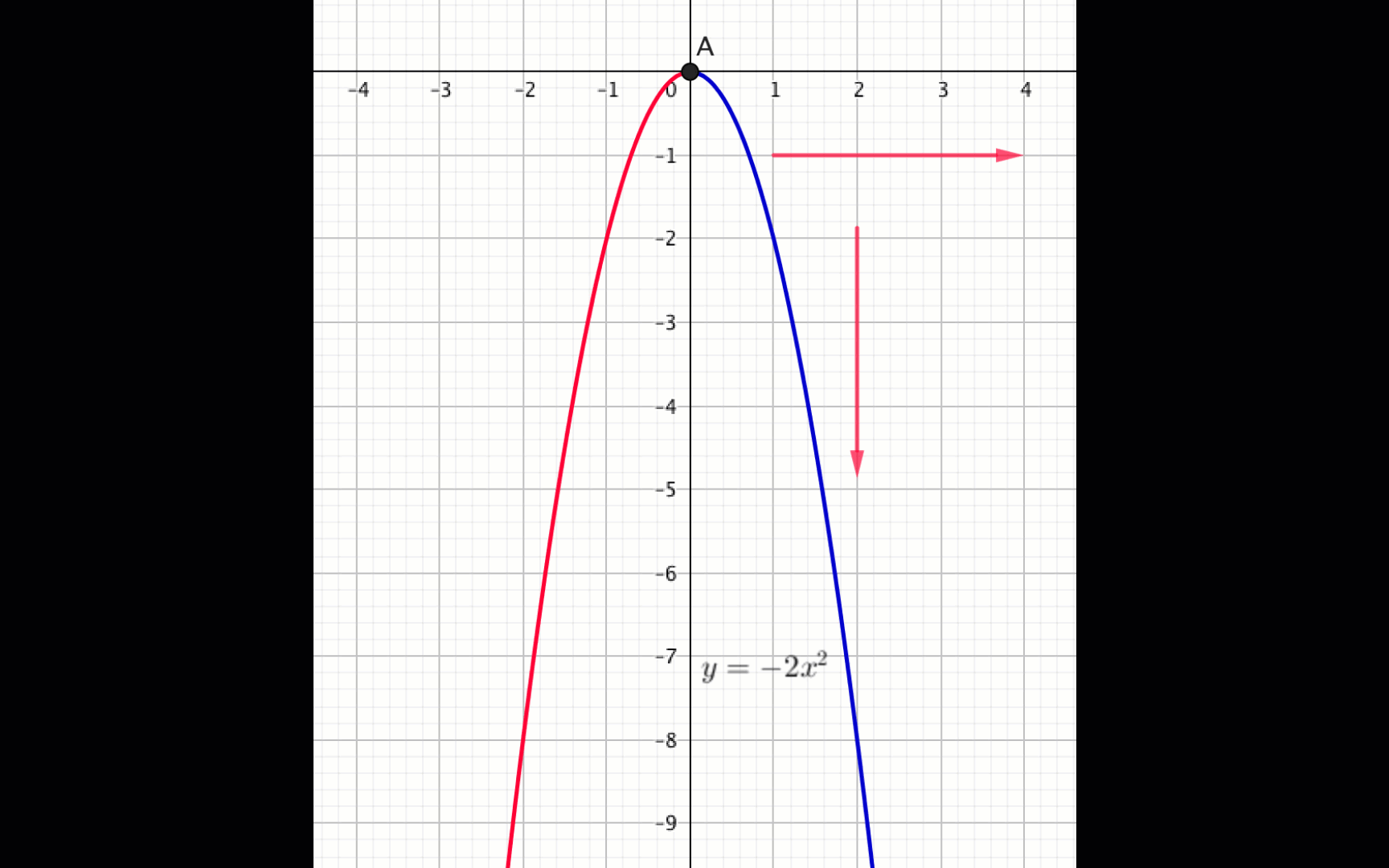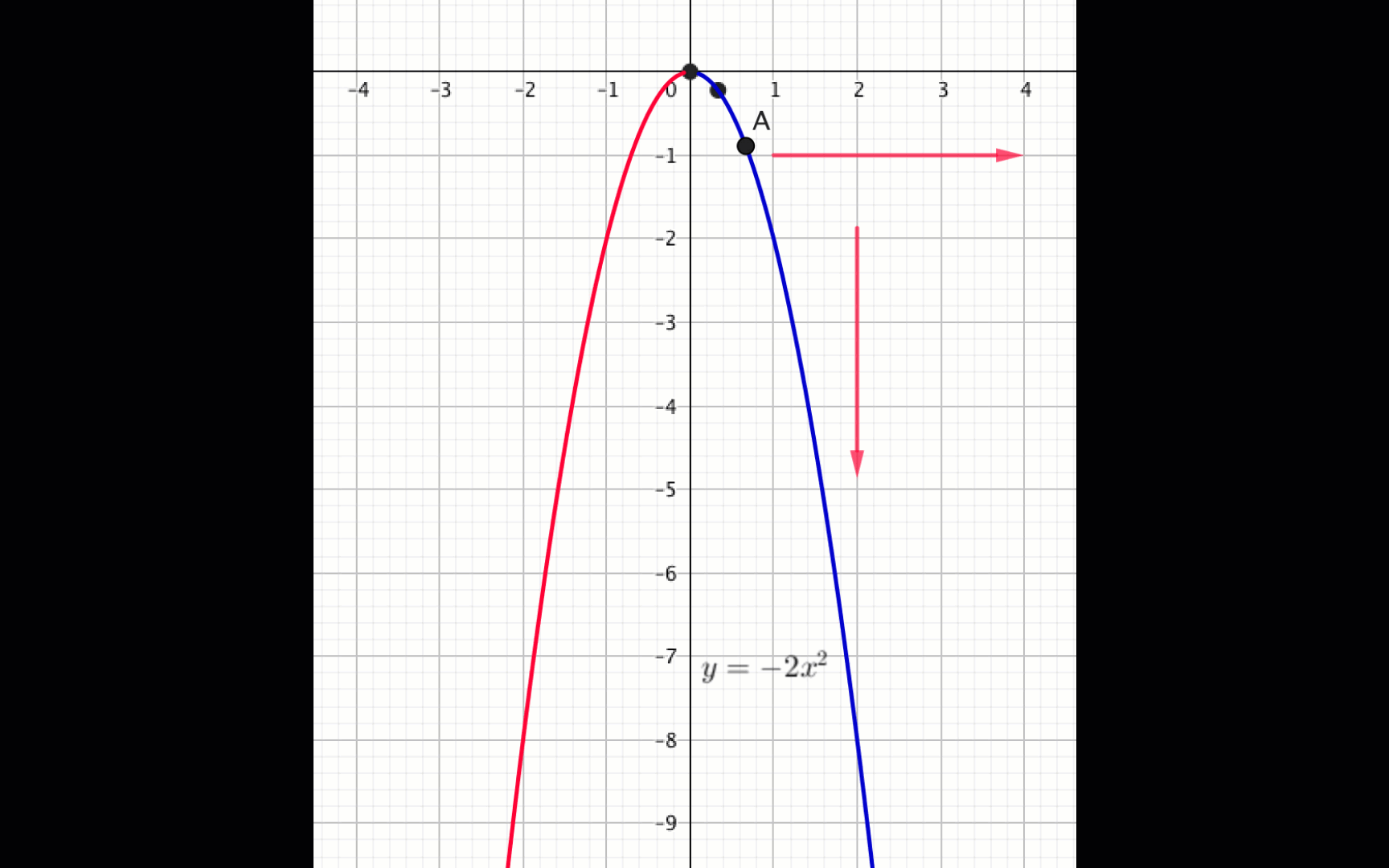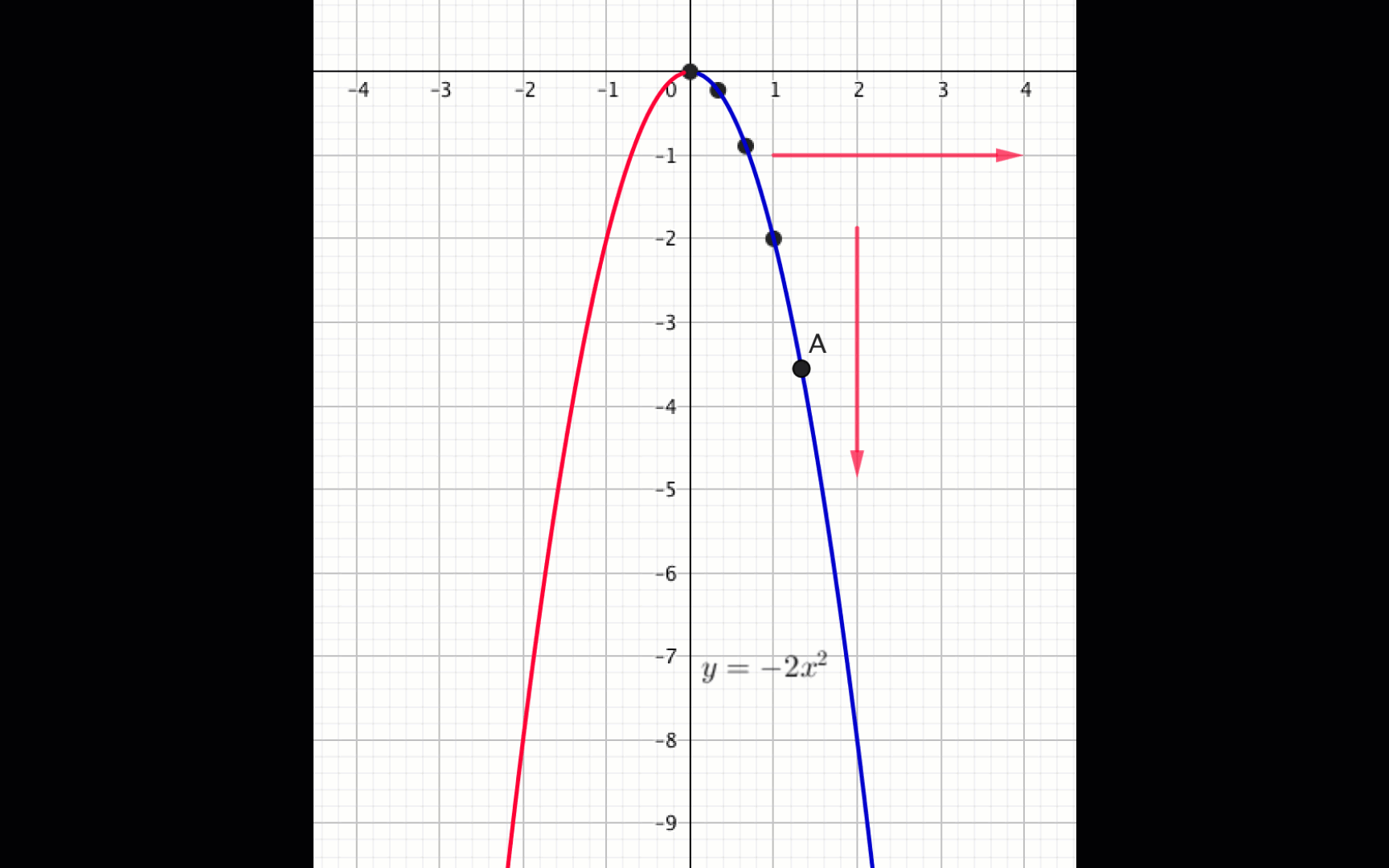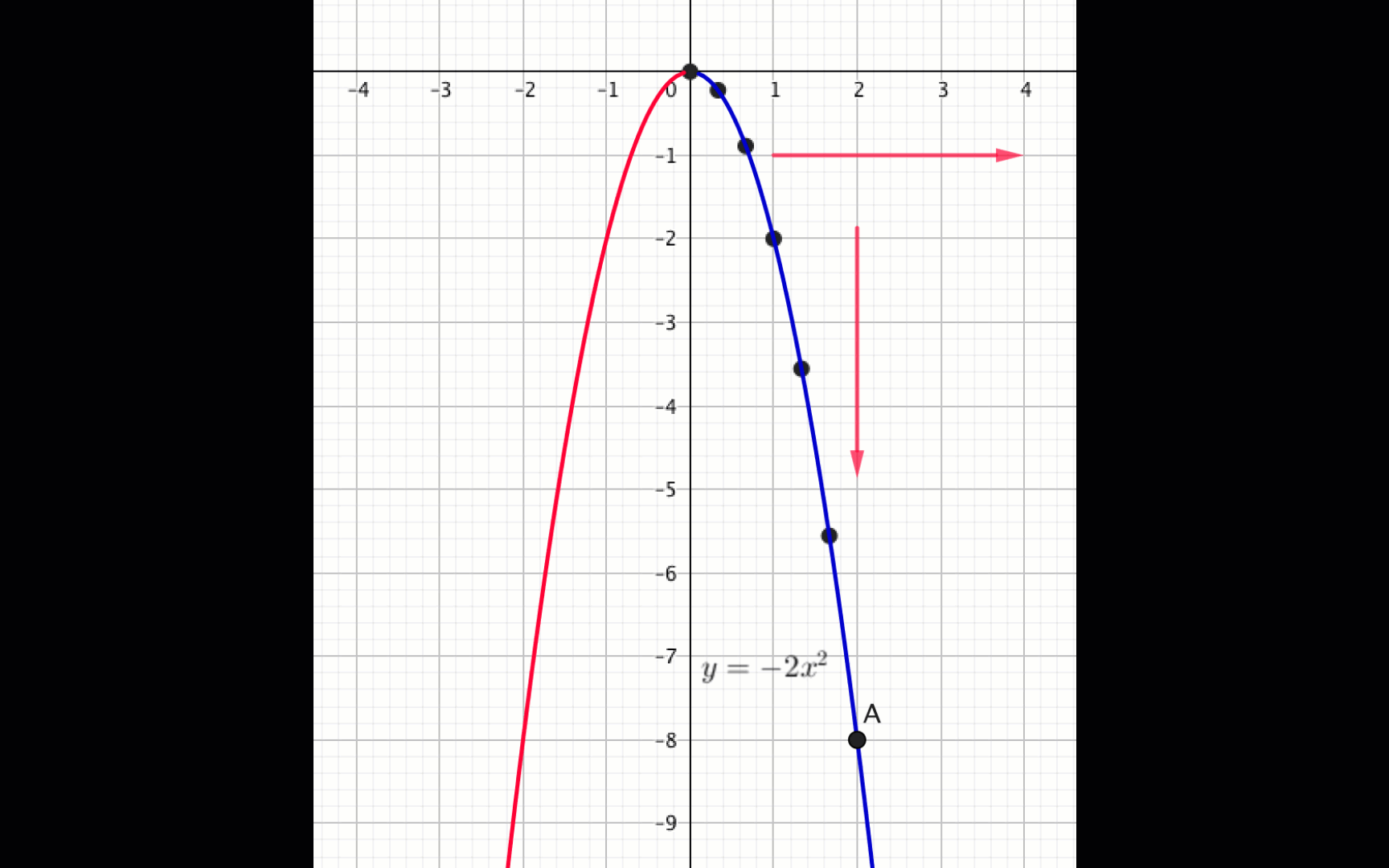
функция \(\displaystyle f(x)=-2x^2\) убывает, если \(\displaystyle x \in (0;\, +\infty){\small .}\)