Задание
Для ввода \(\displaystyle \infty\) используйте меню дополнительного ввода.
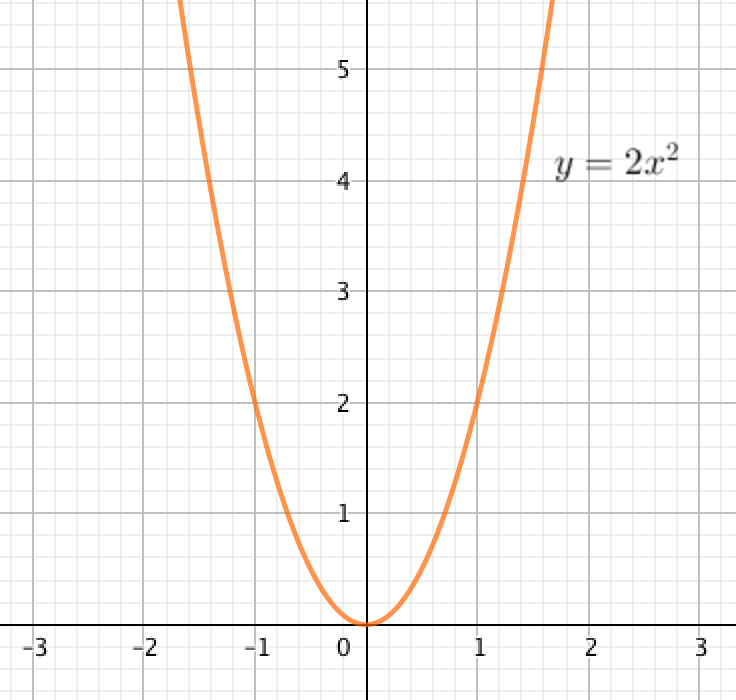
Опираясь на график квадратичной функции \(\displaystyle y=2x^2{\small , }\) найдите её промежутки возрастания и убывания.
Убывает, если \(\displaystyle x \in \Big(\)
\(\displaystyle ;\)
\(\displaystyle \Big)\)
Возрастает, если \(\displaystyle x \in \Big(\)
\(\displaystyle ;\)
\(\displaystyle \Big)\)
Для ввода \(\displaystyle \infty\) используйте меню дополнительного ввода.

Решение
Правило
Возрастание и убывание функции
Функция \(\displaystyle y=f(x)\) убывает на промежутке \(\displaystyle x \in (a;\, b){\small ,}\)
- если большему значению \(\displaystyle x\) на этом промежутке соответствует меньшее значение функции \(\displaystyle f(x){\small ,}\)
- то есть для любых \(\displaystyle x_1,\, x_2 \in (a;\, b){\small ,}\) если \(\displaystyle x_2>x_1{\small ,}\) то \(\displaystyle f(x_2)<f(x_1){\small .}\)
Из графика видно, что
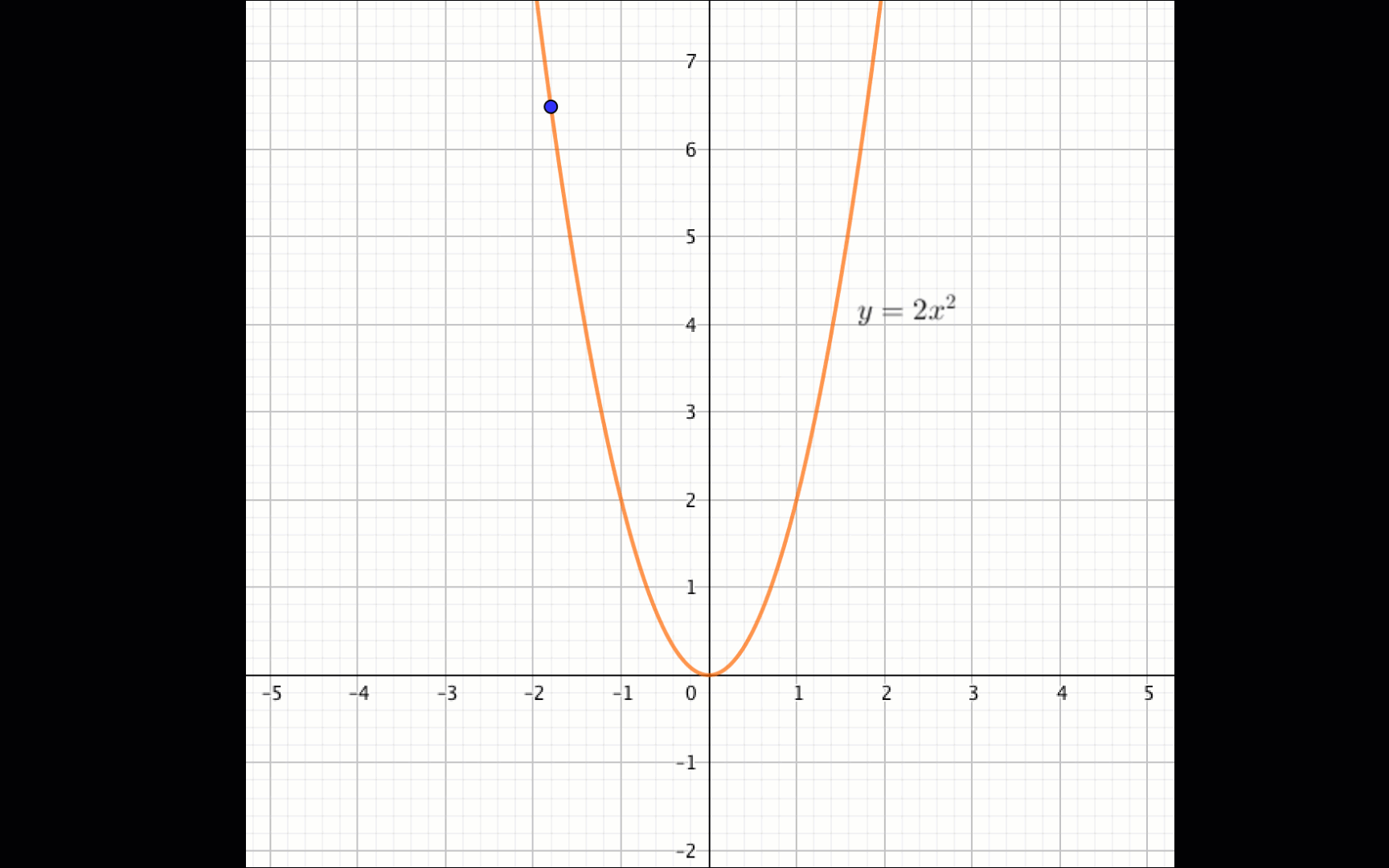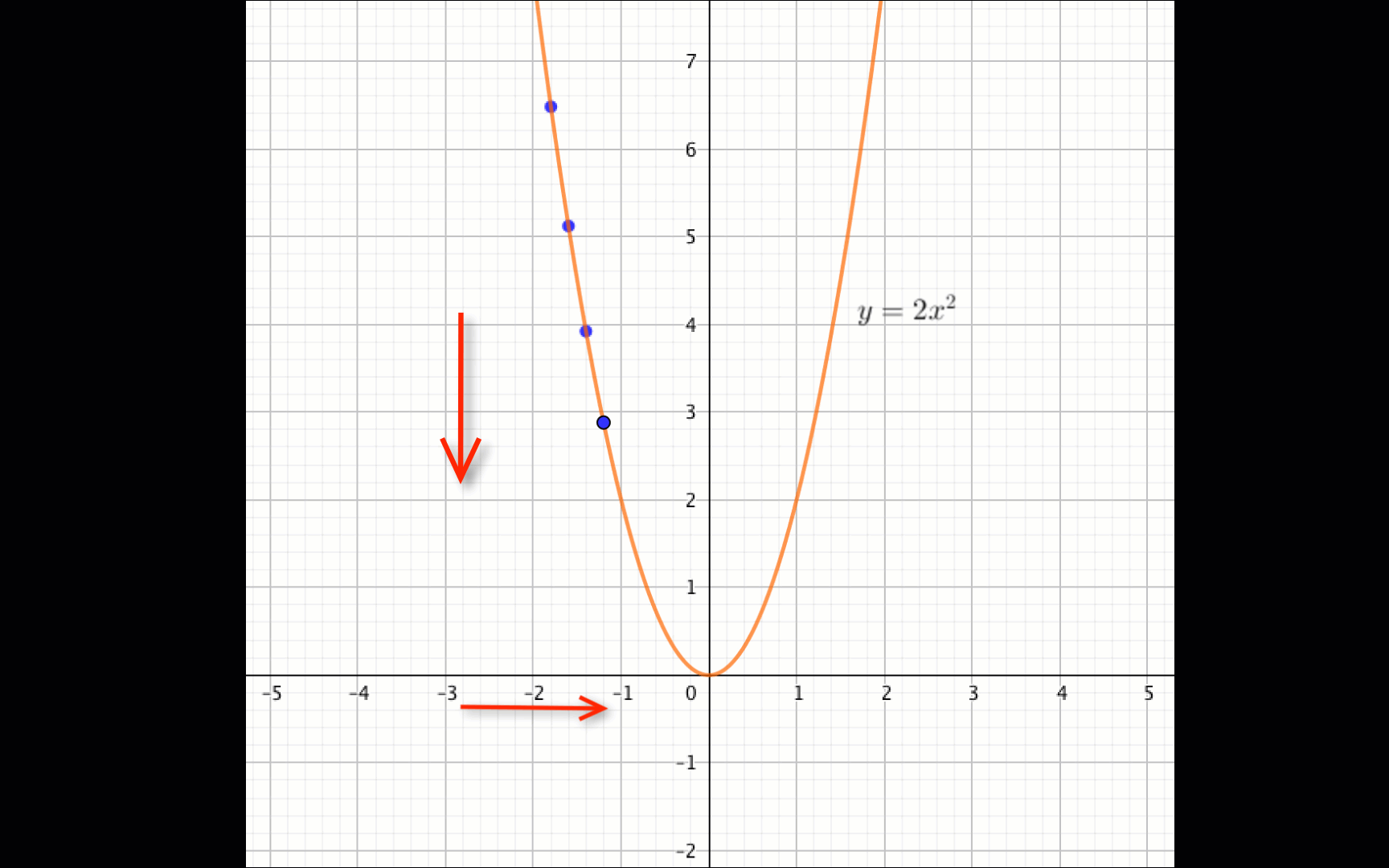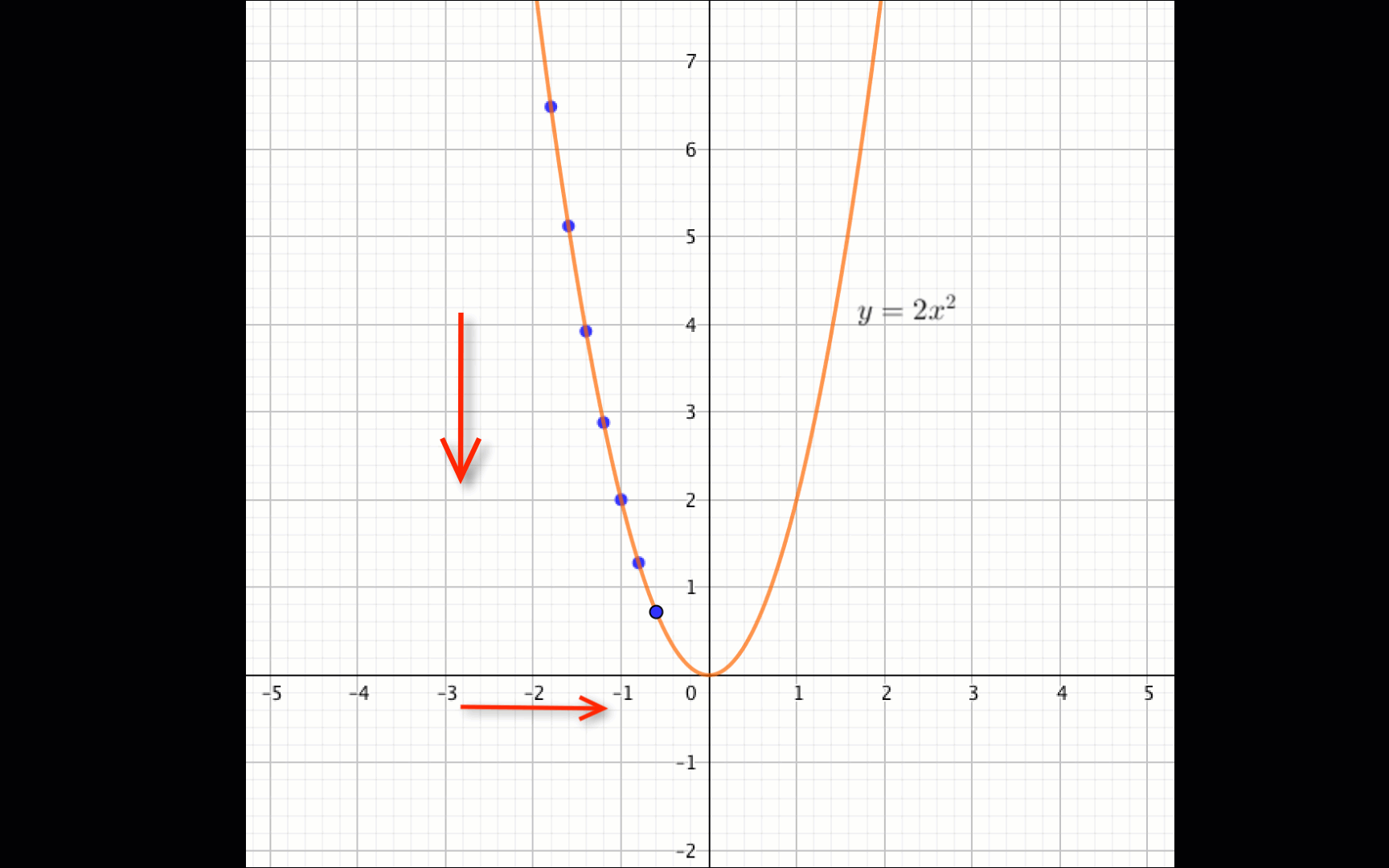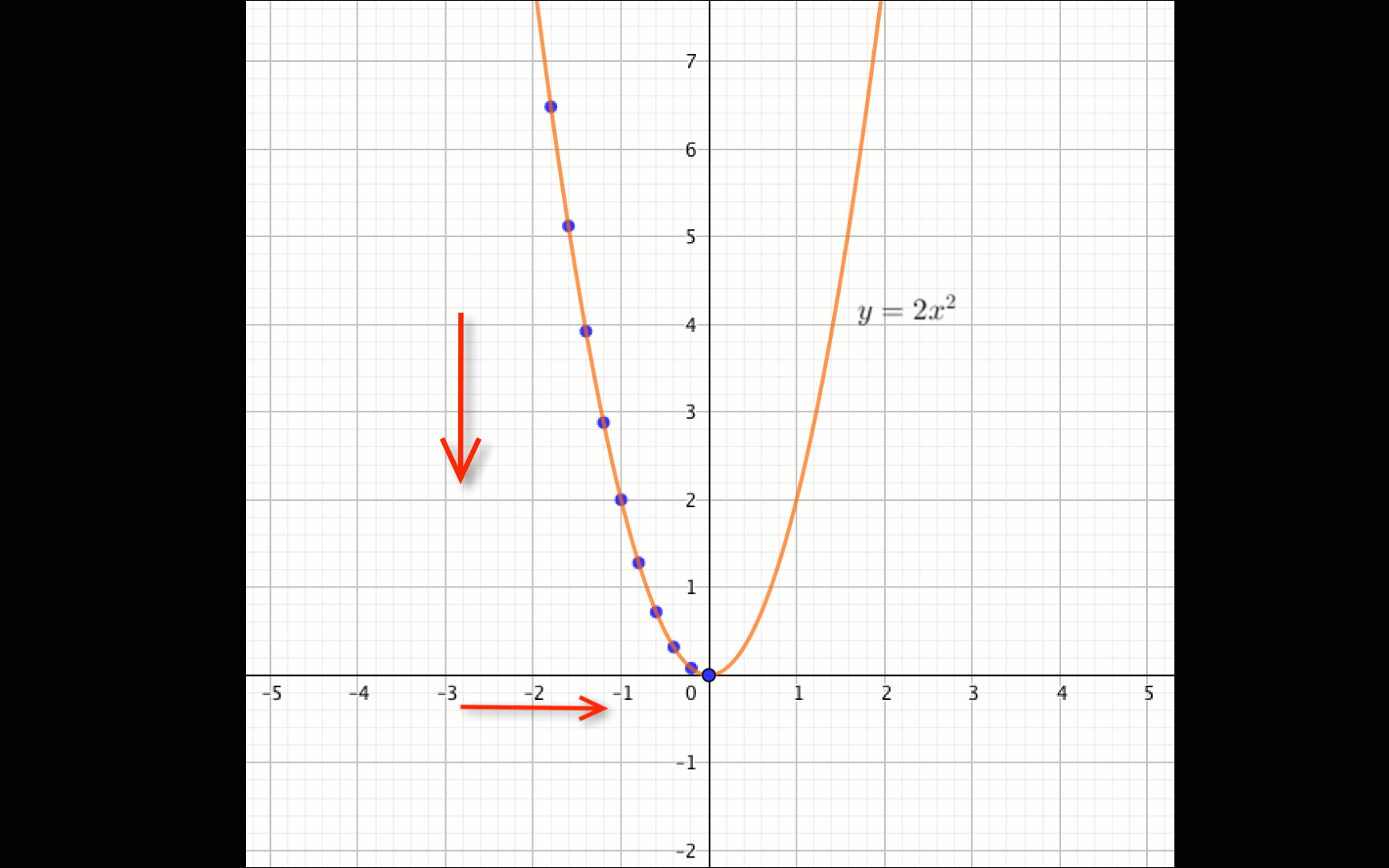
функция \(\displaystyle f(x)=2x^2\) убывает, если \(\displaystyle x \in (-\infty;\, 0){\small .}\)
Алгебраический подход
Правило
Возрастание функции
Функция \(\displaystyle y=f(x)\) возрастает на промежутке \(\displaystyle x \in (a;\, b){\small ,}\)
- если большему значению \(\displaystyle x\) на этом промежутке соответствует большее значение функции \(\displaystyle f(x){\small ,}\)
- то есть для любых \(\displaystyle x_1,\, x_2 \in (a;\, b){\small ,}\) если \(\displaystyle x_2>x_1{\small ,}\) то \(\displaystyle f(x_2)>f(x_1){\small .}\)
Из графика видно, что

функция \(\displaystyle f(x)=2x^2\) возрастает, если \(\displaystyle x \in (0;\, +\infty){\small .}\)
Алгебраический подход