Запишем область определения для функции \(\displaystyle f(x)=9x-\ln \left(9x\right)+3{\small.}\)
Так как \(\displaystyle \ln (9x)\) определен только тогда, когда \(\displaystyle 9x>0{\small,}\) то область определения имеет вид
\(\displaystyle x > 0{\small.}\)
1) Найдем производную функции \(\displaystyle f(x)=9x-\ln \left(9x\right)+3{\small.}\)
\(\displaystyle f^{\prime}(x)=\left(9x-\ln \left(9x\right)+3\right)^{\prime}=9-\frac{1}{x}{\small.}\)
Раскроем скобки. Производная суммы равна сумме производных. То есть
\(\displaystyle\left(9x-\ln \left(9x\right)+3\right)^{\prime}=\left(9x\right)^{\prime}-\left(\ln(9x)\right)^{\prime}+(3)^{\prime}=9-\left(\ln(9x)\right)^{\prime}+0=9-\left(\ln(9x)\right)^{\prime}{\small.}\)
Остается найти производную сложной функции \(\displaystyle \ln(9x){\small.}\)
Сделаем это поэтапно, используя правило.
ПравилоПроизводная сложной функции
\(\displaystyle \left(h({g(x)})\right)^{\prime}=\color{red}{h^{\prime}(g)}\cdot (\color{blue}{g(x)})'{\small.}\)
Задача каждого этапа – свести вычисление производной функции \(\displaystyle h(g(x))\) к вычислению производной более простой функции \(\displaystyle g(x){\small.}\)
Этап 1. Обозначим \(\displaystyle h(g(x))=\ln(9x){\small.}\) Тогда:
\(\displaystyle \boxed{h(\color{blue}{g(x)})=\ln\color{blue}{(9x)}}\longrightarrow\) \(\displaystyle \boxed{ \begin{aligned}&h(x)=\ln(x)\\&\color{blue}{g(x)=9x}\end{aligned}}\longrightarrow\) \(\displaystyle \boxed{\begin{aligned}&h^{\prime}(x)=(\ln(x))^{\prime}=\frac{1}{x}\\&\color{red}{h^{\prime}(g)=\frac{1}{9x}}\end{aligned}} \longrightarrow\)
\(\displaystyle \longrightarrow\boxed{\begin{aligned}\left(\ln(9x)\right)^{\prime}=\color{red}{\frac{1}{9x}}\cdot\left(\color{blue}{9x}\right)^{\prime}\end{aligned}{\small.}}\)
Получили:
\(\displaystyle 9-\left(\ln(9x)\right)^{\prime}=9-{\frac{1}{9x}}\cdot\left({9x}\right)^{\prime}{\small.}\)
Переходим к вычислению производной более простой функции \(\displaystyle 9x{\small.}\)
Этап 2. Так как \(\displaystyle \left({9x}\right)^{\prime}=9\cdot(x)^{\prime}=9\cdot1=9{\small,}\) получаем:
\(\displaystyle 9-\frac{1}{9x}\cdot\left({9x}\right)^{\prime}=9-\frac{1}{9x}\cdot9=9-\frac{1}{x}{\small.}\)
Таким образом, процесс взятия производной функции \(\displaystyle 9x-\ln \left(9x\right)+3\) выглядит следующим образом:
\(\displaystyle \begin{aligned}\left(9x-\ln(9x)+3\right)^{\prime}=9-\left(\ln(9x)\right)^{\prime}=9-\frac{1}{9x}\cdot\left(9x\right)^{\prime}=9-\frac{1}{x}{\small.}\end{aligned}\)
2) Найдем интервалы знакопостоянства \(\displaystyle f^{\prime}(x)=9-\frac{1}{x}{\small.}\)
\(\displaystyle {\left(0;\, \frac{1}{9}\right)}{\small,}\) \(\displaystyle {\left(\frac{1}{9};\,+\infty\right)}\) – интервалы знакопостоянства \(\displaystyle f^{\prime}(x)=9-\frac{1}{x}{\small.}\)
Перепишем функцию в виде дроби:
\(\displaystyle f^{\prime}(x)=9-\frac{1}{x}=\frac{9x-1}{x}{\small.}\)
Найдем корни числителя этого рационального выражения:
\(\displaystyle 9x-1=0{\small,}\)
\(\displaystyle 9x=1{\small,}\)
\(\displaystyle x=\frac{1}{9}{\small.}\)
Найдем корни знаменателя:
\(\displaystyle x=0{ \small .} \)
Отметим корни числителя и знаменателя производной на числовой прямой. Учитывая область определения исходной функции \(\displaystyle x> 0{\small,}\) получаем:
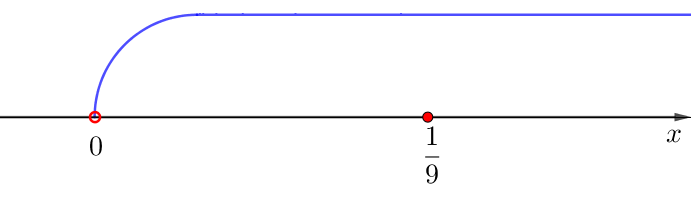
Таким образом, интервалы знакопостоянства производной:
\(\displaystyle {\left(0;\, \frac{1}{9}\right)}{\small,}\) \(\displaystyle {\left(\frac{1}{9};\,+\infty\right)}{\small.}\)
3) Определим знаки производной на получившихся интервалах.
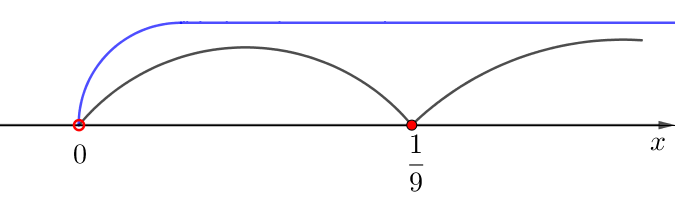
- на интервале \(\displaystyle \color{green}{\left(\frac{1}{9};\, +\infty\right)}\) функция \(\displaystyle f^{\prime}(x)>0{\small,}\)
- на интервале \(\displaystyle \textcolor{blue}{\left(0;\,\frac{1}{9}\right)}\) функция \(\displaystyle f^{\prime}(x)<0{\small.}\)
Определим знак функции \(\displaystyle f^{\prime}(x)=9-\frac{1}{x}\) на каждом из интервалов:
\(\displaystyle \color{blue}{\left(0;\, \frac{1}{9}\right)}{\small,}\) \(\displaystyle \textcolor{green}{\left(\frac{1}{9};\,+\infty\right)}{\small.}\)
Для этого выберем по точке на каждом из интервалов и определим в этой точке знак функции. Получаем:
- для \(\displaystyle \color{blue}{x=\frac{1}{10} \in \left(0;\, \frac{1}{9}\right)}\) знак \(\displaystyle f^{\prime}\left(\color{blue}{\frac{1}{10}}\right)=9-\frac{1}{\frac{1}{10}}=9-10\color{red}{<}0{\small ;}\)
- для \(\displaystyle \color{green}{x=1 \in{\left(\frac{1}{9};\,+\infty\right)}}\) знак \(\displaystyle f^{\prime}\left(\color{green}{1}\right)=9-\frac{1}{1}=9-1\color{red}{>}0{\small .}\)
Значит,
- на интервале \(\displaystyle \color{green}{\left(\frac{1}{9};\, +\infty\right)}\) функция \(\displaystyle f^{\prime}(x)>0{\small,}\)
- на интервале \(\displaystyle \textcolor{blue}{\left(0;\,\frac{1}{9}\right)}\) функция \(\displaystyle f^{\prime}(x)<0{\small.}\)
Отмечая знаки производной на картинке, получаем:
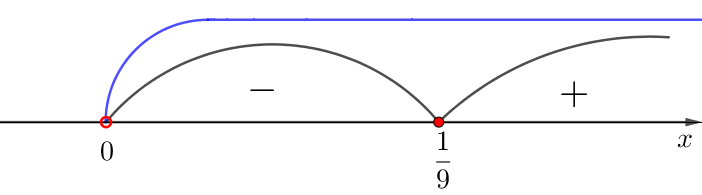
4) Определим промежутки возрастания и убывания функции \(\displaystyle f(x)=9x-\ln \left(9x\right)+3{\small ,}\) пользуясь правилом.
ПравилоЕсли для любой точки \(\displaystyle x_0\in(a;\,b)\) производная \(\displaystyle f'(x_0)\) существует и \(\displaystyle f'(x_0)>0{\small,}\) то
функция \(\displaystyle f(x)\) возрастает \(\displaystyle \nearrow\) на всем интервале \(\displaystyle (a;\,b){\small.}\)
Если для любой точки \(\displaystyle x_0\in(a;\,b)\) производная \(\displaystyle f'(x_0)\) существует и \(\displaystyle f'(x_0)<0{\small,}\) то
функция \(\displaystyle f(x)\) убывает \(\displaystyle \searrow\) на всем интервале \(\displaystyle (a;\,b){\small.}\)
Зная знаки производной \(\displaystyle f'(x){\small,}\) определим промежутки возрастания и убывания \(\displaystyle f(x){\small:}\)
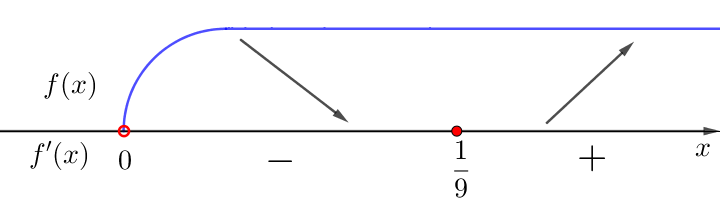
Схематически изобразим \(\displaystyle f(x){\small:}\)
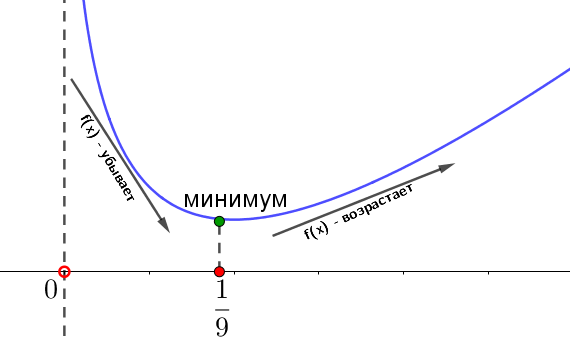
Точка \(\displaystyle x=\frac{1}{9}\) принадлежит области определения \(\displaystyle f(x){\small.}\)
Значит, \(\displaystyle x=\frac{1}{9}\) – точка минимума функции \(\displaystyle f(x)=9x-\ln \left(9x\right)+3{\small.}\)
5) Определим, в какой из точек промежутка \(\displaystyle \left[\frac{1}{18};\,\frac{5}{18}\right]\) достигается наименьшее значение.
Отметим на картинке интервал \(\displaystyle \left[\frac{1}{18};\,\frac{5}{18}\right]{\small:}\)
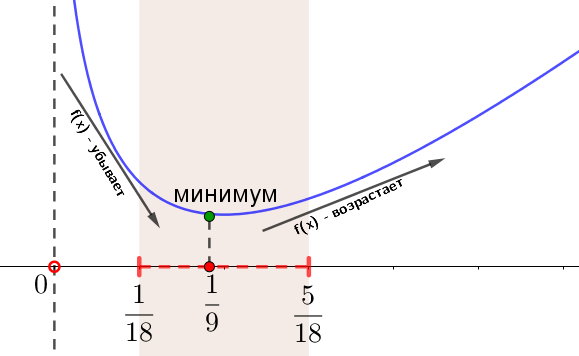
Видно, что на отрезке \(\displaystyle \left[\frac{1}{18};\,\frac{5}{18}\right]\) функция убывает до точки \(\displaystyle x=\frac{1}{9}{\small,}\) а затем возрастает.
Значит, наименьшее значение доcтигается в точке \(\displaystyle {x=\frac{1}{9}}{\small.}\)
Вычислим значение в этой точке:
\(\displaystyle f\left(\frac{1}{9}\right)=9\cdot\frac{1}{9}-\ln \left(9\cdot\frac{1}{9}\right)+3=1-0+3=4{\small.}\)
Ответ: \(\displaystyle 4{\small.}\)