На рисунке изображён график функции \(\displaystyle y=f\left(x\right){\small.}\) На оси абсцисс отмечены точки \(\displaystyle -2{\small,}\, -1{\small,}\, 1{\small,}\, 2{\small.}\) Расположите отмеченные точки в порядке убывания значения производной.
Определим, как ведет себя функция в окрестности точек \(\displaystyle -2{\small,}\, -1{\small,}\, 1{\small,}\, 2{\small:}\)
Получаем:
| Точки | Поведение функции в окрестности | Значение производной в точке |
| \(\displaystyle -2,\, 2\) | \(\displaystyle f(x)\) возрастает | \(\displaystyle f^{\prime}(x)\ge0\) |
| \(\displaystyle -1, 1\) | \(\displaystyle f(x)\) убывает | \(\displaystyle f^{\prime}(x)\le0\) |
При этом ни в одной из отмеченных точек касательная не параллельна оси \(\displaystyle \rm OX\). Значит, знаки неравенств в таблице строгие:
| Точки | Значение производной в точке |
| \(\displaystyle -2,\, 2\) | \(\displaystyle f^{\prime}(x)>0\) |
| \(\displaystyle -1, 1\) | \(\displaystyle f^{\prime}(x)<0\) |
То есть значения производной в точках \(\displaystyle -2\) и \(\displaystyle 2\) больше значений производной в точках \(\displaystyle -1\) и \(\displaystyle 1{\small.}\)
Сравним сначала значения производной в точках \(\displaystyle -2{\small,}\) \(\displaystyle 2{ \small ,}\) а затем в точках \(\displaystyle -1{\small,}\) \(\displaystyle 1{\small.}\)
1. Рассмотрим точки \(\displaystyle -2\) и \(\displaystyle 2{\small.}\)
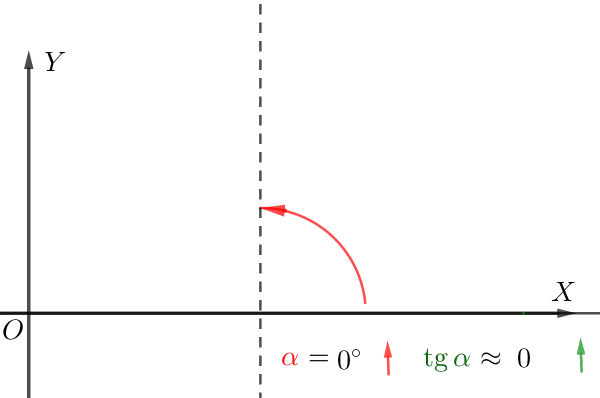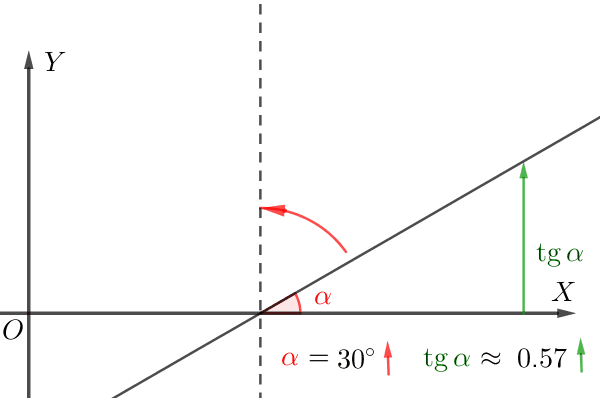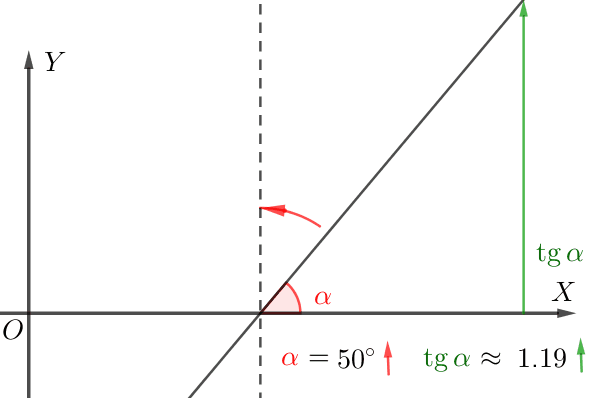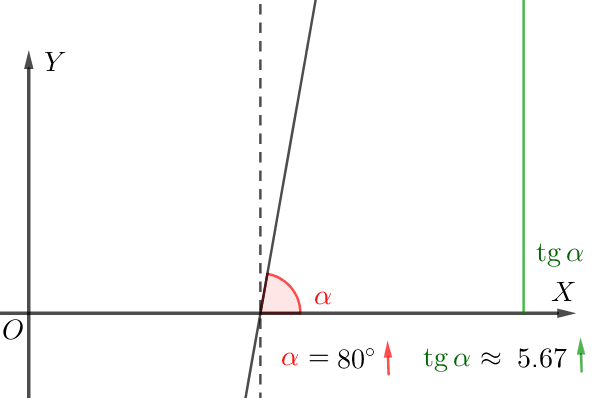
Значение производной в точке \(\displaystyle x_0\) равно \(\displaystyle \tg(\alpha){ \small ,}\) где \(\displaystyle \alpha\) – угол наклона касательной в соответствующей точке на кривой \(\displaystyle y=f(x){\small .}\)
Поэтому, чтобы сравнить значение производной в точках \(\displaystyle -2\) и \(\displaystyle 2{ \small ,}\) воспользуемся правилом:
Если касательная образует острый угол с положительным направлением оси \(\displaystyle \rm OX{\small,}\) то
чем больше угол наклона, тем больше тангенс.
Построим касательные в точках \(\displaystyle -2\) и \(\displaystyle 2{\small:}\)
Из рисунка видно, угол наклона касательной \(\displaystyle \color{green}{\alpha}\) больше, чем угол наклона касательной \(\displaystyle \color{red}{\beta}{\small.}\)
Значит, тангенс угла \(\displaystyle \color{green}{\alpha}\) больше, чем тангенс угла \(\displaystyle \color{red}{\beta}{\small.}\)
Соответственно, производная больше в точке \(\displaystyle -2{\small :}\)
\(\displaystyle f^{\prime}(-2)>f^{\prime}(2)>0{\small.}\)
2. Рассмотрим точки \(\displaystyle -1\) и \(\displaystyle 1{\small.}\)
Чтобы сравнить значение производной в точках \(\displaystyle -1\) и \(\displaystyle 1{ \small ,}\) воспользуемся правилом:
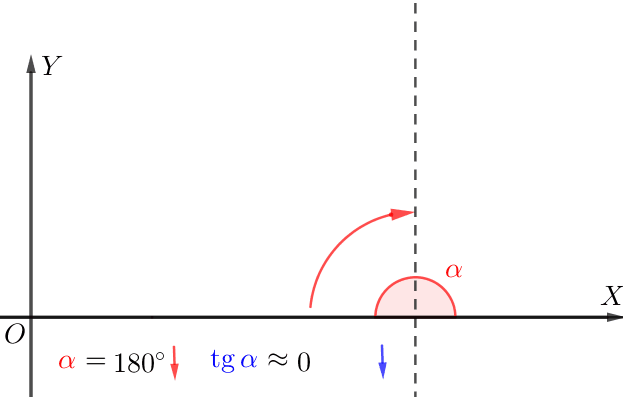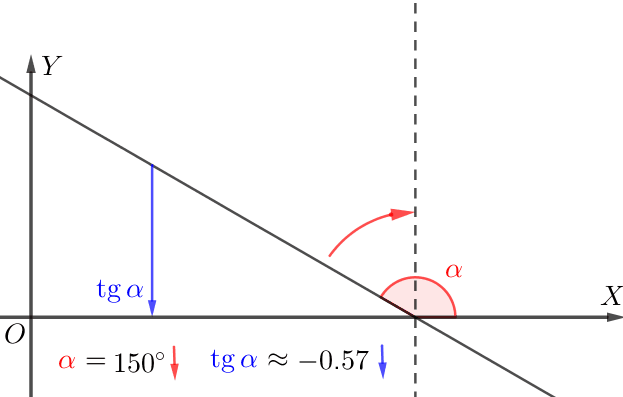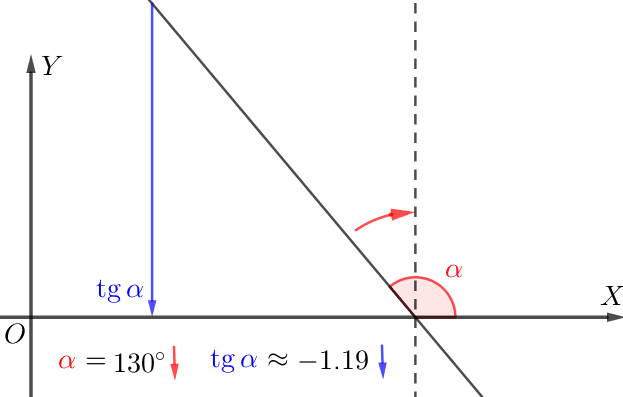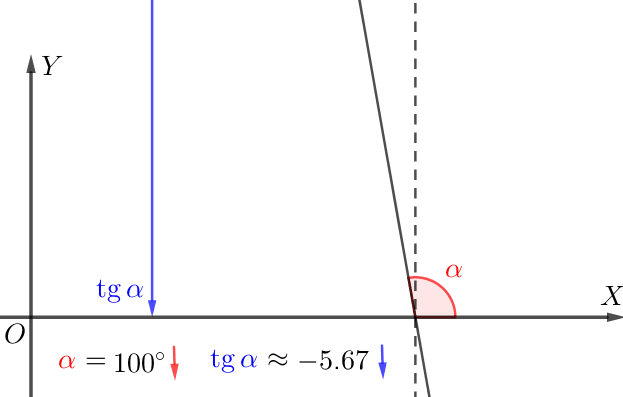
Если касательная образует тупой угол с положительным направлением оси \(\displaystyle \rm OX{\small,}\) то
чем меньше угол наклона, тем меньше тангенс.
Построим касательные в точках \(\displaystyle -1\) и \(\displaystyle 1{\small:}\)
Сравним угол наклона касательной \(\displaystyle \color{#7F00FF}{\gamma}\) и угол наклона касательной \(\displaystyle \delta{\small.}\)
В точке \(\displaystyle -1\) касательная более "вертикальна" (наклонена меньше), чем касательная в точке \(\displaystyle 1 {\small .}\)
Поэтому угол наклона касательной \(\displaystyle \color{#7F00FF}{\gamma}\) меньше, чем угол наклона касательной \(\displaystyle \delta{\small.}\)
Значит, \(\displaystyle \tg\color{#7F00FF}{\gamma}\) меньше \(\displaystyle \tg\delta\) и, соответственно, производная меньше в точке \(\displaystyle -1{\small:}\)
\(\displaystyle f^{\prime}(-1)<f^{\prime}(1)<0{\small.}\)
Таким образом, получаем:
\(\displaystyle f^{\prime}(-2)>f^{\prime}(2)>0>f^{\prime}(1)>f^{\prime}(-1){\small.}\)
Значит, в порядке убывания значения производной точки располагаются:
\(\displaystyle -2,\,2,\,1,\,-1{\small.}\)