Значения синуса и косинуса для специальных значений углов:
| Угол | \(\displaystyle \sin\) | \(\displaystyle \cos\) |
| \(\displaystyle 0\) | \(\displaystyle \sin 0=0\) | \(\displaystyle \cos 0=1 \) |
| \(\displaystyle \frac{\pi}{2}\) | \(\displaystyle \sin\frac{\pi}{2}=1\) | \(\displaystyle \cos\frac{\pi}{2}=0 \) |
| \(\displaystyle \pi\) | \(\displaystyle \sin\pi=0\) | \(\displaystyle \cos\pi=-1 \) |
| \(\displaystyle \frac{3\pi}{2}\) | \(\displaystyle \sin\frac{3\pi}{2}=-1\) | \(\displaystyle \cos\frac{3\pi}{2}=0 \) |
По свойству единичной тригонометрической окружности, точка на окружности, которую дает центральный угол величины \(\displaystyle \alpha{ \small ,}\) имеет координаты \(\displaystyle (\cos\alpha;\, \sin\alpha){\small : }\)
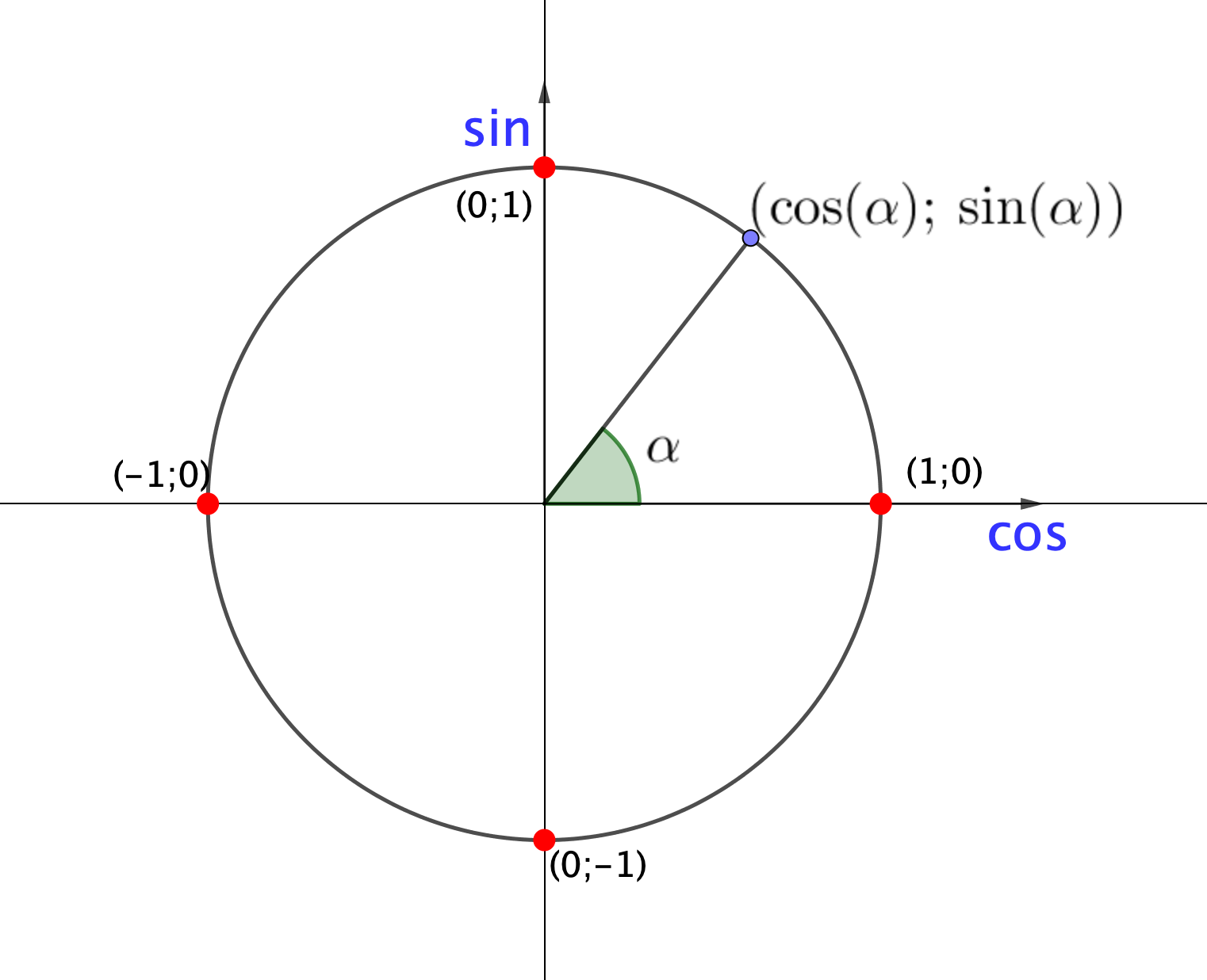
Тогда:
1) Точка, образованная углом величины \(\displaystyle \bf 0{ \small ,}\) имеет координаты \(\displaystyle (1;\, 0){\small .}\) Следовательно,

\(\displaystyle \sin 0=0\) и \(\displaystyle \cos 0=1{\small .}\)
2) Точка, образованная углом величины \(\displaystyle \bf \frac{\pi}{2}{ \small ,}\) имеет координаты \(\displaystyle (0;\, 1){\small .}\) Следовательно,

\(\displaystyle \sin\frac{\pi}{2}=1\) и \(\displaystyle \cos\frac{\pi}{2}=0{\small .}\)
3) Точка, образованная углом величины \(\displaystyle \pi{ \small ,}\) имеет координаты \(\displaystyle (-1;\, 0){\small .}\) Следовательно,
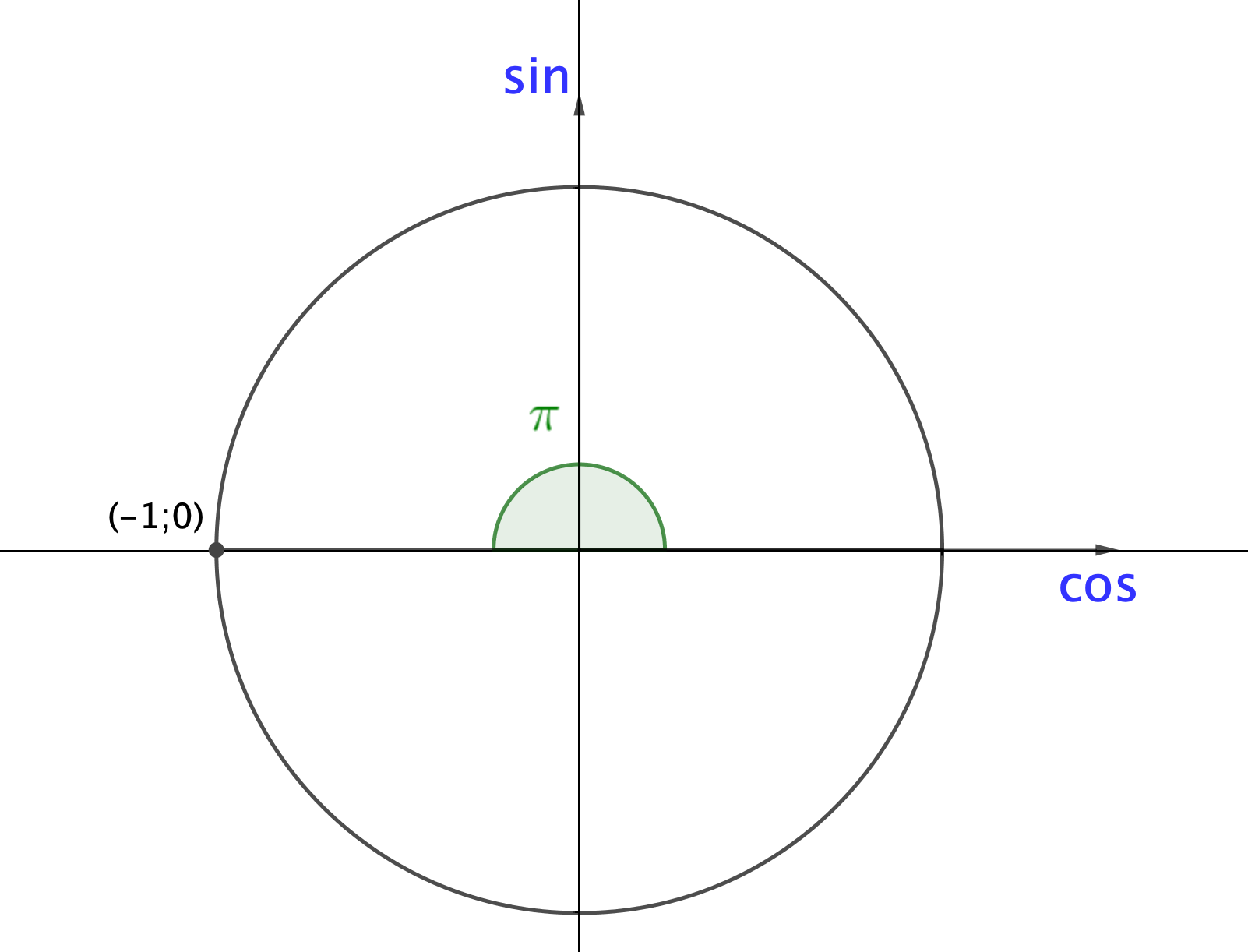
\(\displaystyle \sin\pi=0\) и \(\displaystyle \cos\pi=-1{\small .}\)
4) Точка, образованная углом величины \(\displaystyle \bf \frac{3\pi}{2}{ \small ,}\) имеет координаты \(\displaystyle (0;\, -1){\small .}\) Следовательно,
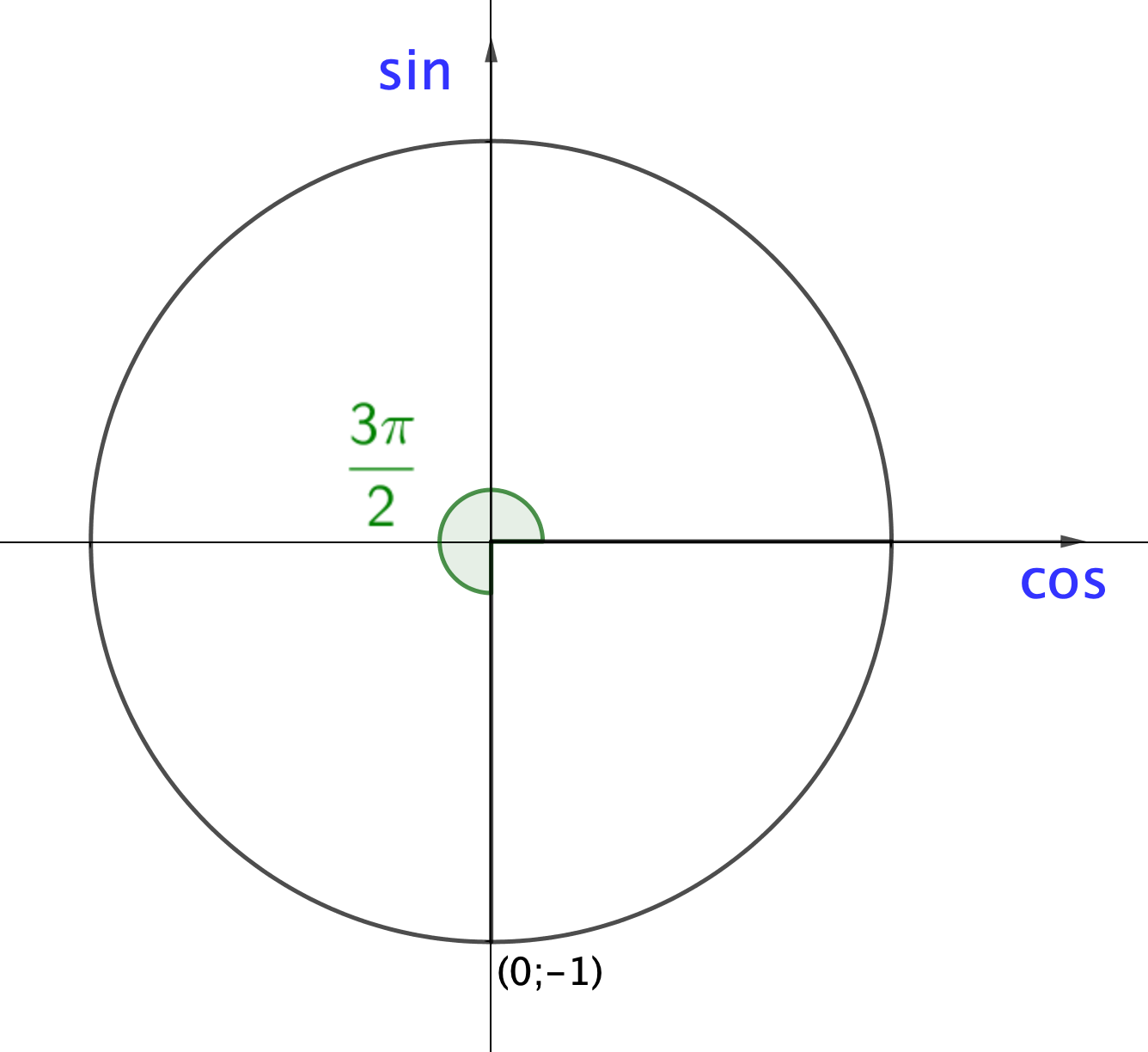
\(\displaystyle \sin\frac{3\pi}{2}=-1\) и \(\displaystyle \cos\frac{3\pi}{2}=0{\small .}\)