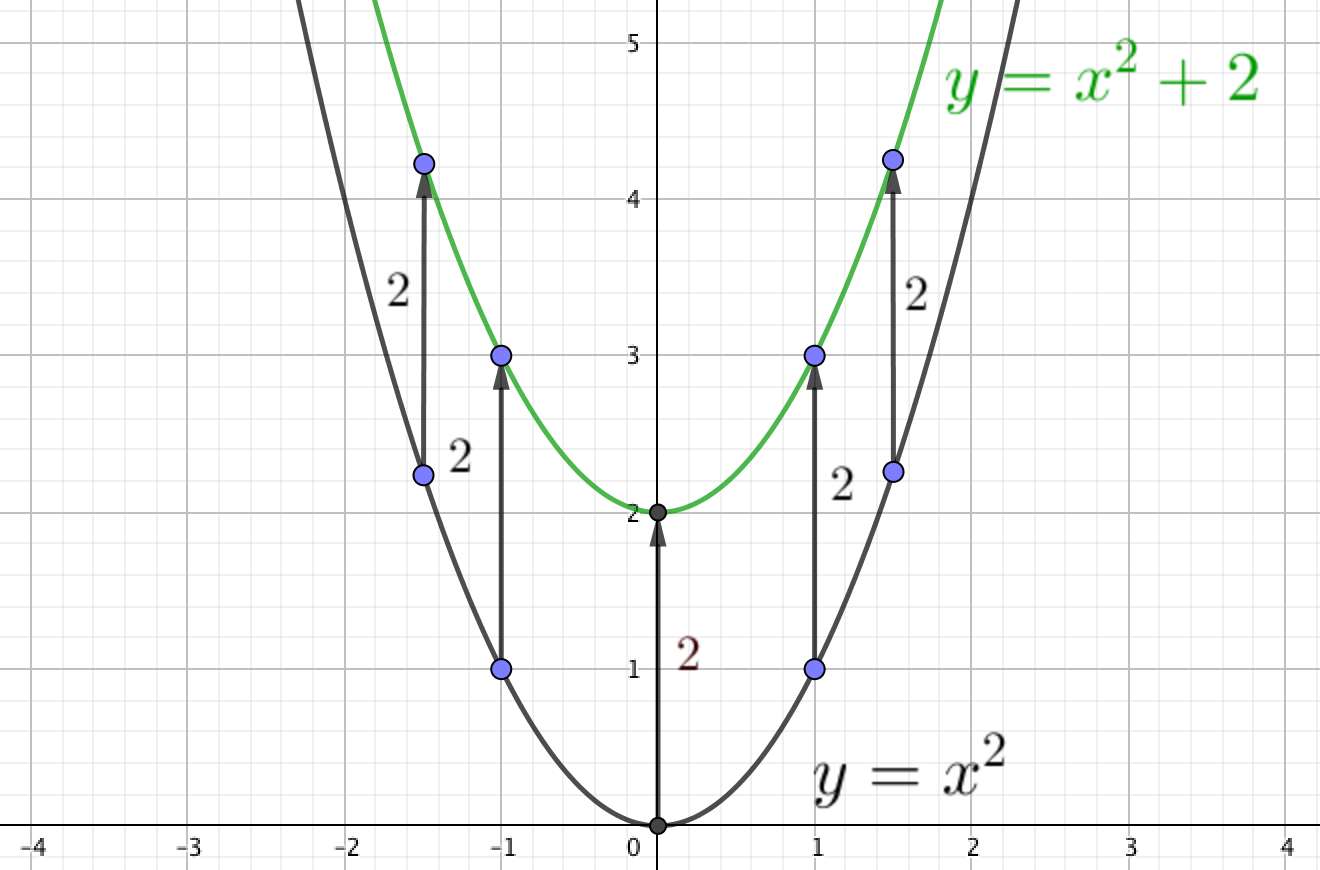
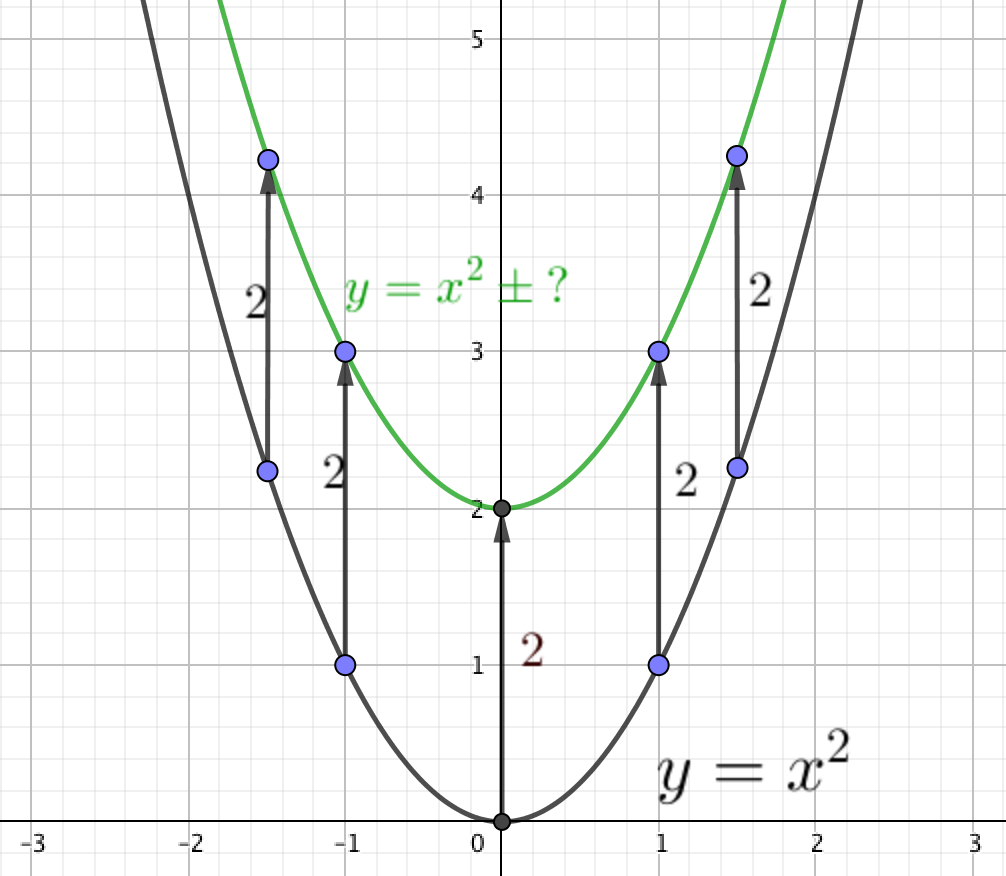
Запишите уравнение параболы, полученной с помощью сдвига параболы \(\displaystyle y=x^2\) на \(\displaystyle 2\) единицы вверх (вдоль оси \(\displaystyle \rm OY\)).
\(\displaystyle \color{green}{y=x^2}\)
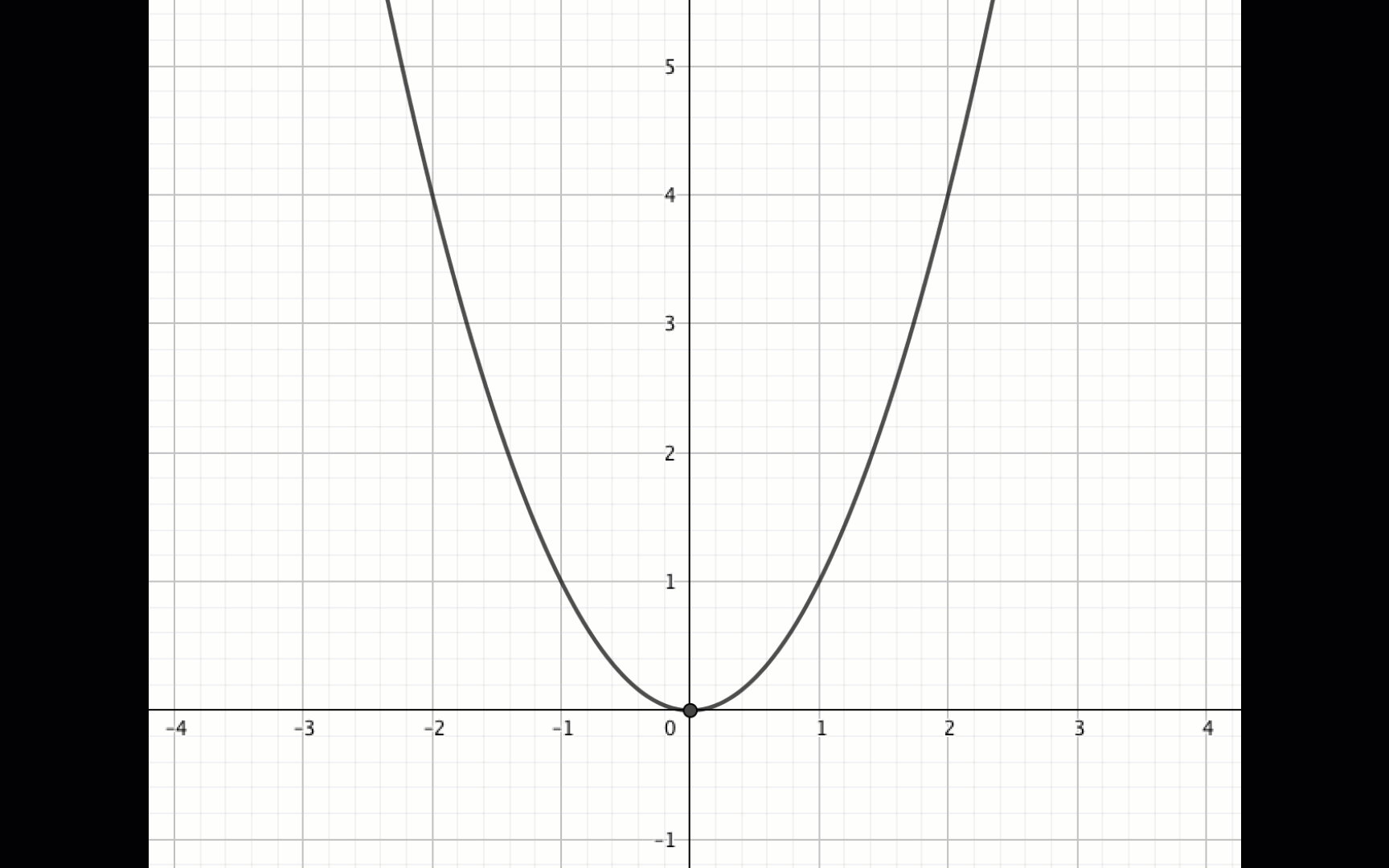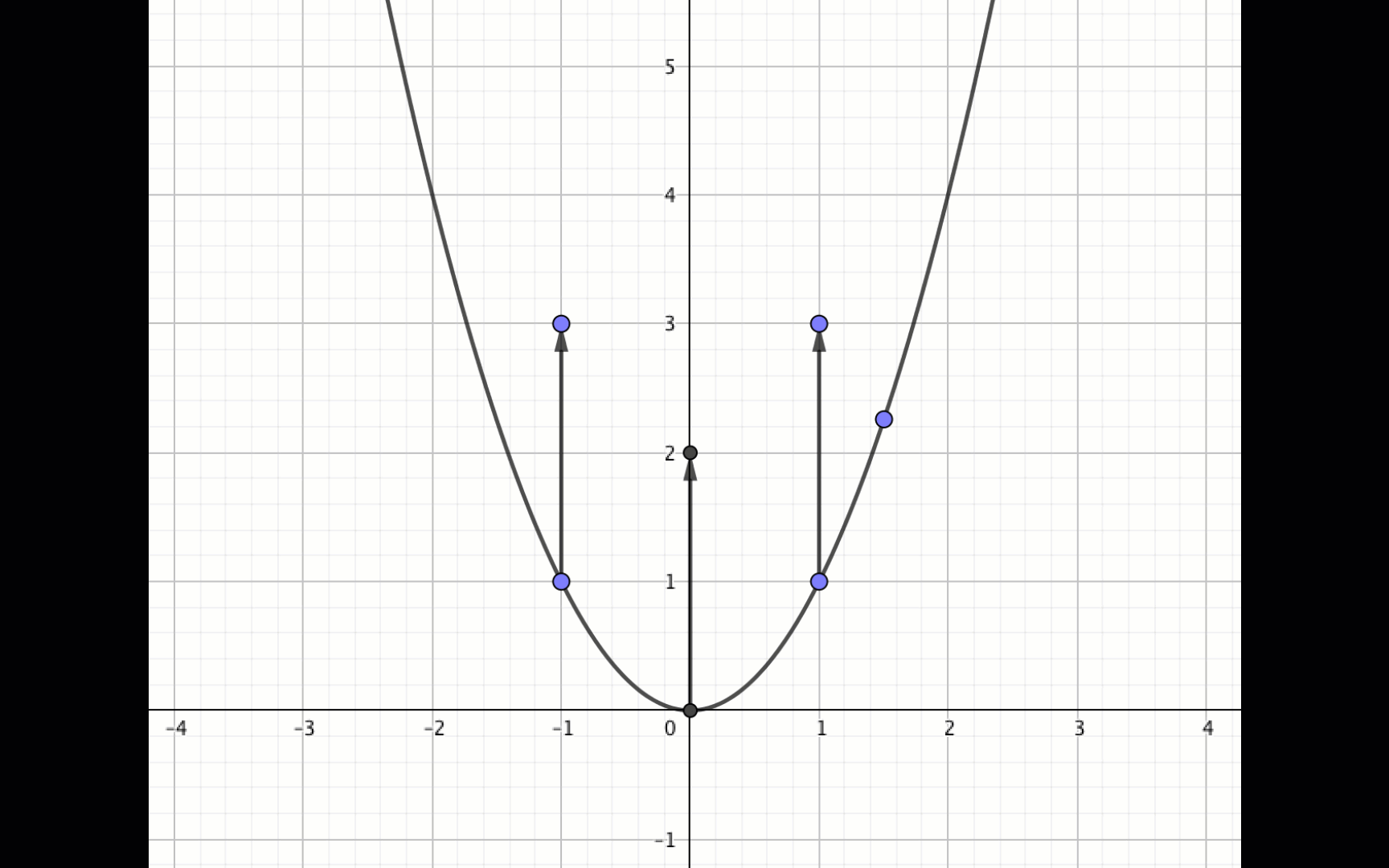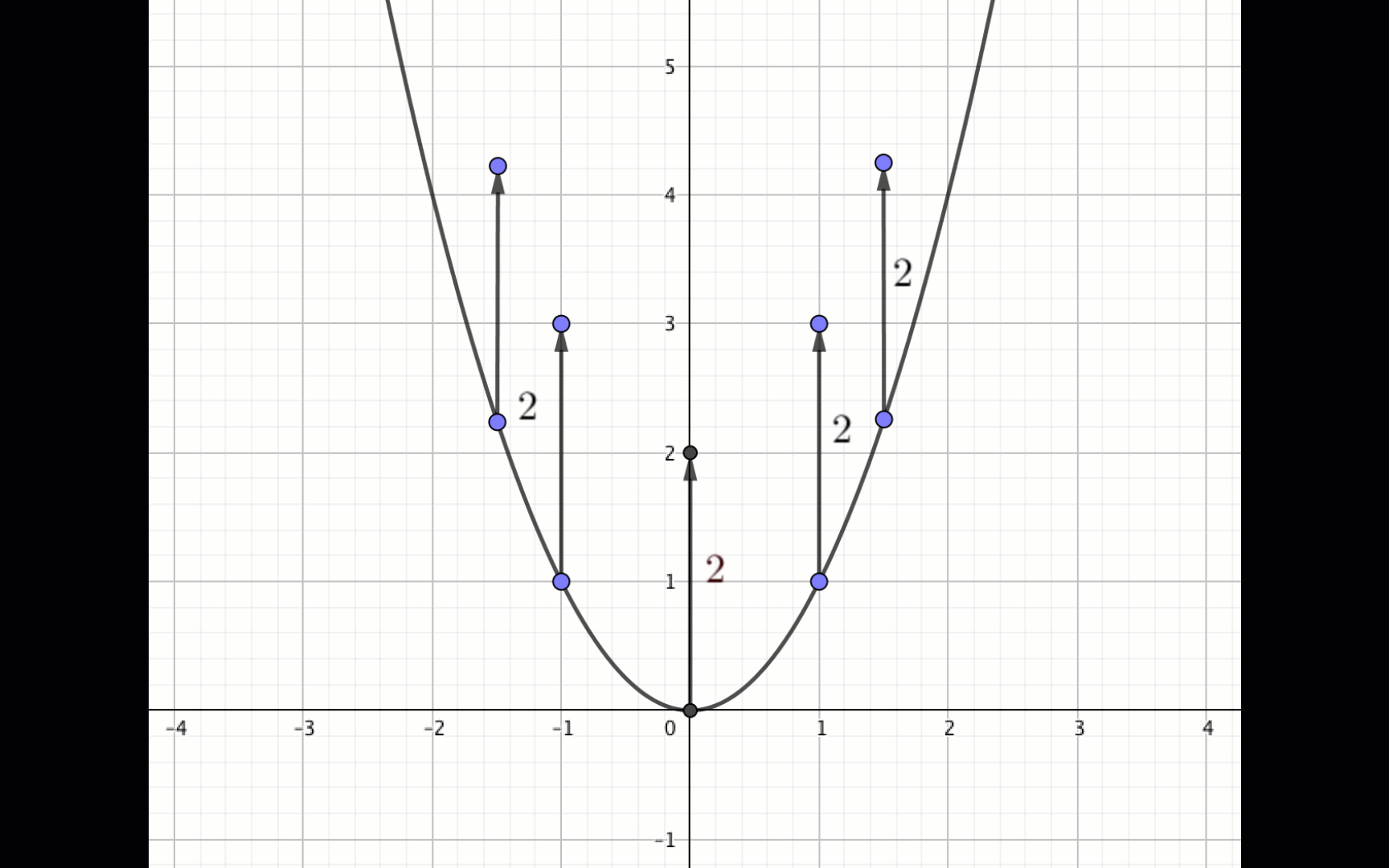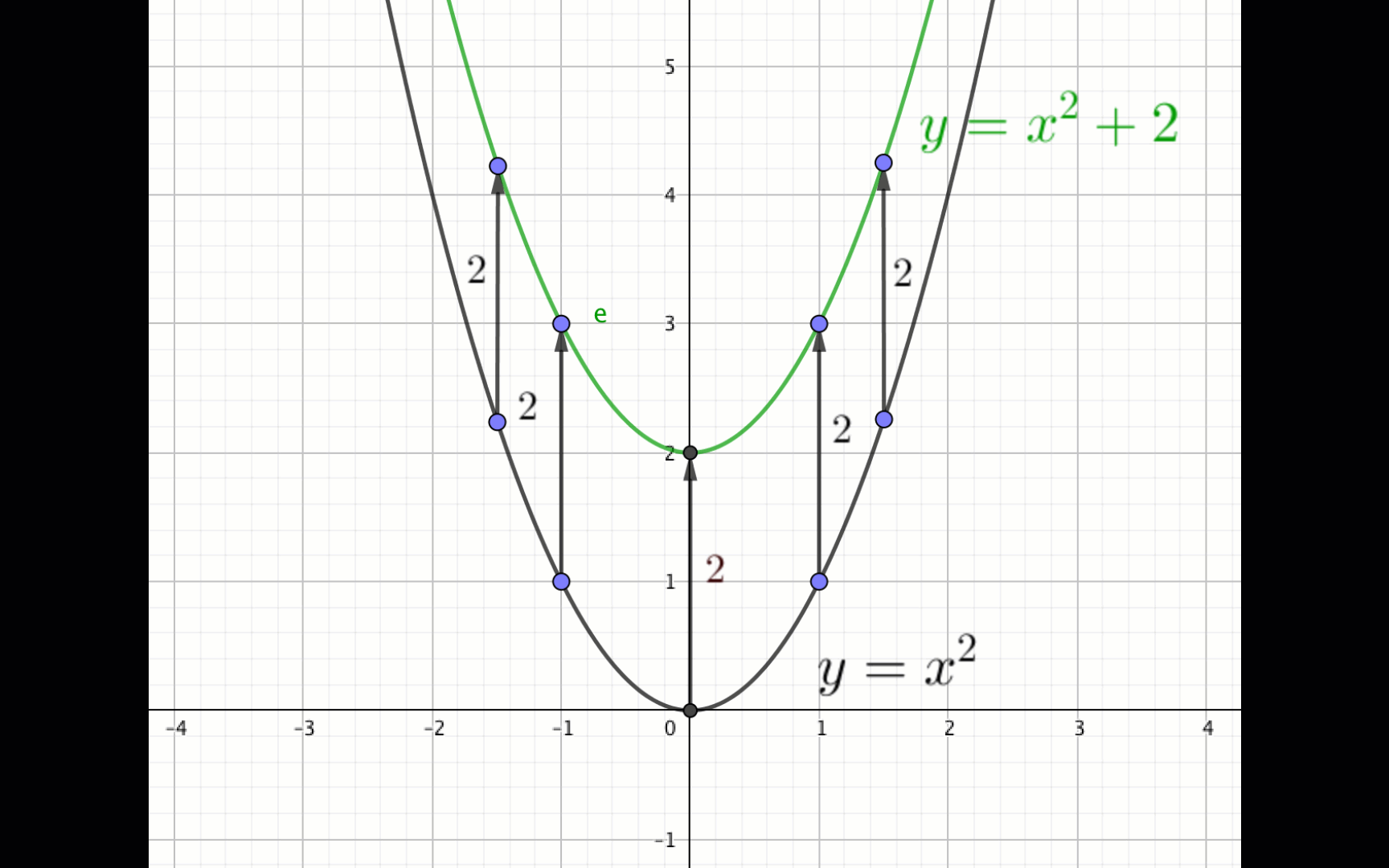
Если некоторую точку с координатами \(\displaystyle (x_0\,; y_0)\) сдвинуть на \(\displaystyle \color{red}{A}\) единиц вверх вдоль оси \(\displaystyle \rm OY\), то получим точку с координатами \(\displaystyle (x_0\,; y_0+\color{red}{A}){\small :}\)

Пусть
\(\displaystyle x^{\prime}=x_0\) и \(\displaystyle y^{\prime}=y_0+\color{red}{A}{\small ,}\)
тогда
\(\displaystyle \color{blue}{x_0}=\color{blue}{x^{\prime}}\) и \(\displaystyle \color{green}{y_0}=\color{green}{y^{\prime}}-\color{red}{A}{\small .}\)
Поэтому, если в \(\displaystyle \color{green}{y_0}=f(\color{blue}{x_0})\) заменить \(\displaystyle \color{blue}{x_0}\) на \(\displaystyle \color{blue}{x^{\prime}}\) и \(\displaystyle \color{green}{y_0}\) на \(\displaystyle \color{green}{y^{\prime}}- \color{red}{A}{ \small ,}\) то получаем
\(\displaystyle \color{green}{y^{\prime}}- \color{red}{A}=f(\color{blue}{x^{\prime}})\)
или
\(\displaystyle \color{green}{y^{\prime}}=f(\color{blue}{x^{\prime}})+ \color{red}{A}{\small .}\)
Таким образом,
каждая точка после сдвига на \(\displaystyle \color{red}{A}\) единиц вверх вдоль оси \(\displaystyle \rm OY\) удовлетворяет уравнению
\(\displaystyle y=f(x)+\color{red}{A}{\small .}\)
Поэтому можно сформулировать правило.
Если график функции \(\displaystyle y=f(x) \) сдвинуть на \(\displaystyle \color{red}{\rm A} \) единиц вверх, то получится график функции \(\displaystyle y=f(x)+\color{red}{\rm A}{\small . } \)
Нам дан график функции \(\displaystyle y=x^2{\small . } \) Мы его двигаем на \(\displaystyle \color{red}{2}\) единицы вверх.
Тогда, согласно правилу, у нас получится график функции
\(\displaystyle y= x^2+\color{red}{2}{\small . }\)