На графике показана зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат – крутящий момент в Н\(\displaystyle \cdot \)м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее \(\displaystyle 20\) Н\(\displaystyle \cdot \)м. Определите по графику, какого наименьшего числа оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение?
По условию
- число оборотов двигателя в минуту откладывается на оси абсцисс (горизонтальная ось);
- значения крутящего момента откладываются на оси ординат (вертикальная ось).
Известно, что автомобиль может начать движение, если крутящий момент будет не менее \(\displaystyle 20\) Н\(\displaystyle \cdot \)м.
Нужно определить, при каком наименьшем числе оборотов двигателя в минуту автомобиль может начать движение.
Из условия следует, что автомобиль может начать двигаться, когда крутящий момент впервые достигнет \(\displaystyle 20\) Н\(\displaystyle \cdot \)м. Найдём число оборотов двигателя, соответствующее данному значению крутящего момента. Тем самым ответим на вопрос задачи.
На оси ординат отметим точку \(\displaystyle \color{blue}{20}\) и проведём через неё горизонтальную прямую.
Все точки пересечения графика с этой прямой соответствуют крутящему моменту двигателя \(\displaystyle 20\) Н\(\displaystyle \cdot \)м.
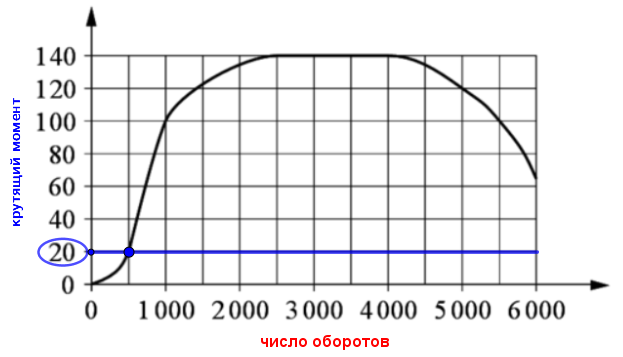
Видим, что такая точка только одна.
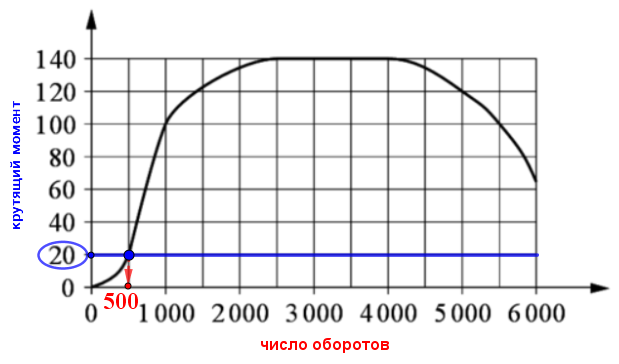
Число оборотов двигателя, которое ей сответствует находится посередине между \(\displaystyle 0\) и \(\displaystyle 1000{\small.}\)
То есть это \(\displaystyle \color{red}{500}{\small}\) оборотов в минуту.
Итак, наименьшее наименьшее число оборотов двигателя в минуту, при котором автомобиль может начать движение, равно \(\displaystyle 500{\small .}\)
Ответ: \(\displaystyle 500{\small.}\)