В треугольнике \(\displaystyle ABC\) угол \(\displaystyle C\) равен \(\displaystyle 90^{\circ}{\small , }\) \(\displaystyle CB=8\) и \(\displaystyle \sin\angle A=0{,}5{\small .}\)
Найдите длину отрезка \(\displaystyle HB{\small .}\)
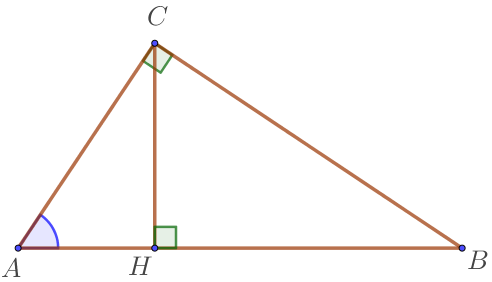
Так как сумма острых углов в прямоугольном треугольнике равна \(\displaystyle 90^{\circ} \small, \) то \(\displaystyle \angle A +\angle B =90^{ \circ} \small.\) Тогда \(\displaystyle \sin \angle A = \sin(90^{\circ}-\angle B)=\cos \angle B \small.\) | 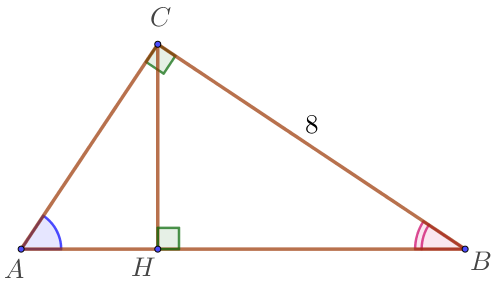 |
Рассмотрим прямоугольный треугольник \(\displaystyle CBH\small.\)
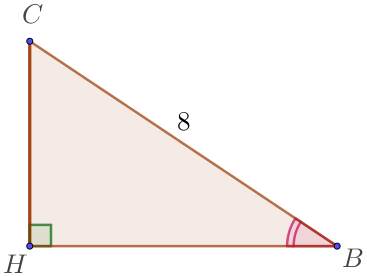 | По определению косинуса \(\displaystyle \cos \angle B =\frac{BH}{CB}\small. \) То есть \(\displaystyle 0{,}5=\frac{BH}{8} \small, \) \(\displaystyle BH=0{,}5 \cdot 8 \small, \) \(\displaystyle BH=4 \small. \) |
Ответ: \(\displaystyle 4 \small. \)