В треугольнике \(\displaystyle ABC\) угол \(\displaystyle C\) равен \(\displaystyle 90^{\circ},\) длина стороны \(\displaystyle AB=5,\) \(\displaystyle \sin A=\frac{7}{25}.\)
Найдите длину стороны \(\displaystyle AC\small. \)
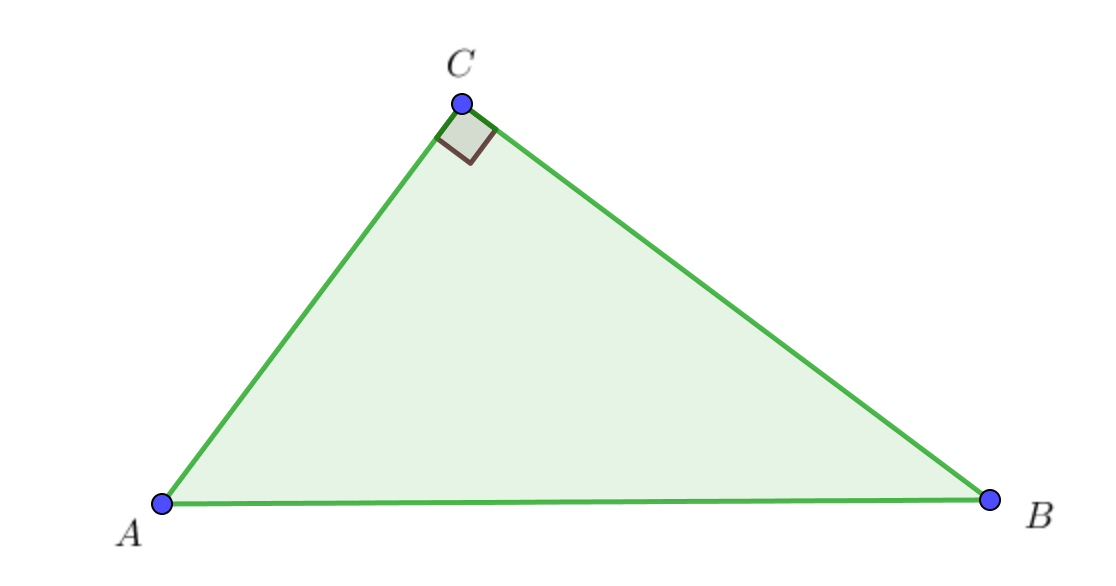
По определению
\(\displaystyle \sin A=\frac{CB}{AB}{\small .} \)
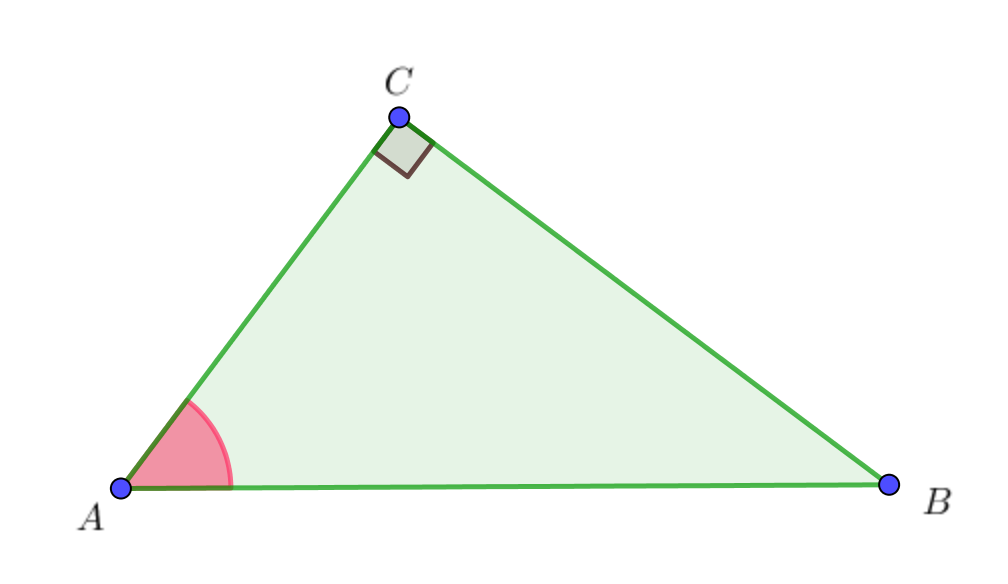
Подставим известные величины \(\displaystyle AB=5{\small , }\) \(\displaystyle \sin A =\frac{7}{25}: \)
\(\displaystyle \frac{7}{25}=\frac{CB}{5}{\small .}\)
Отсюда
\(\displaystyle CB=5\cdot \frac{7}{25}=\frac{7}{5}{\small .}\)
По теореме Пифагора \(\displaystyle AC^2+CB^2=AB^2{\small .}\) Тогда
\(\displaystyle AC^2+\left(\frac{7}{5}\right)^2=5^2{\small .}\)
Отсюда
\(\displaystyle AC^2=5^2-\left(\frac{7}{5}\right)^2{\small .}\)
Ответ:\(\displaystyle 4{,}8{\small .}\)