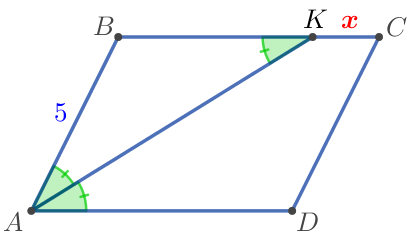
В параллелограмме \(\displaystyle ABCD\) проведена биссектриса угла \(\displaystyle A {\small,}\) пересекающая сторону \(\displaystyle BC\) в точке \(\displaystyle K {\small.}\) Найдите \(\displaystyle KC {\small,}\) если \(\displaystyle AB=5 {\small,}\) а периметр параллелограмма равен \(\displaystyle 22 {\small.} \)
Пусть \(\displaystyle \color{red}x\) – длина отрезка \(\displaystyle KC {\small,}\) тогда \(\displaystyle \color{red}x=BC-BK {\small.}\) | 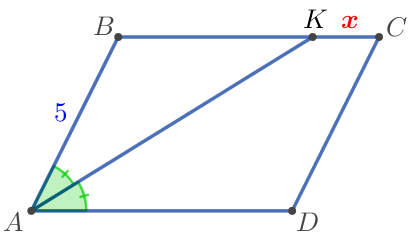 |
Найдем длины отрезков \(\displaystyle BC\) и \(\displaystyle BK {\small.} \)
По условию периметр параллелограмма \(\displaystyle ABCD\) равен \(\displaystyle 22 {\small,} \) \(\displaystyle AB=5 {\small.} \)
\(\displaystyle P_{ABCD}=2 \cdot (AB+BC) {\small,}\)
\(\displaystyle 22=2 \cdot (5+BC) {\small,}\)
\(\displaystyle 5+BC= 11{\small,}\)
\(\displaystyle BC=11-5=6 {\small.}\)
В параллелограмме \(\displaystyle ABCD {\small:}\)
|
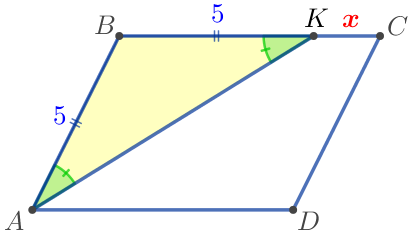
По условию \(\displaystyle AK\) – биссектриса, значит \(\displaystyle \angle KAD= \angle KAB{\small.}\) Следовательно, \(\displaystyle \angle KAB= \angle AKB{\small.}\) |
Рассмотрим треугольник \(\displaystyle ABK {\small:}\)
| Так как в треугольнике \(\displaystyle ABK\) углы при основании равны, то \(\displaystyle \triangle ABK\) – равнобедренный. Значит, \(\displaystyle BK=AB=5 {\small.}\) |
Получаем
\(\displaystyle \color{red}x=BC-BK=6-5=1 {\small.}\)
Ответ: \(\displaystyle 1 {\small.}\)