Прямые \(\displaystyle m\) и \(\displaystyle n\) параллельны (см. рисунок). Найдите \(\displaystyle \angle 3 {\small,}\) если \(\displaystyle \angle 1 =66^{\circ} {\small,}\) \(\displaystyle \angle 2=88^{\circ} {\small.}\) Ответ дайте в градусах.

\(\displaystyle ^{\circ}\)
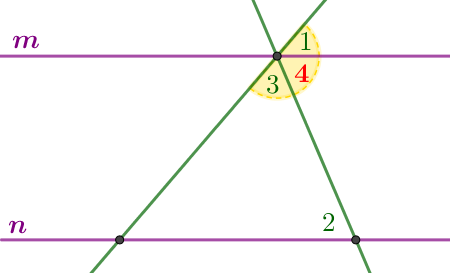 | Обозначим на рисунке угол \(\displaystyle {\color {red} 4} {\small.}\) Углы \(\displaystyle 1 {\small,}\) \(\displaystyle 3\) и \(\displaystyle {\color {red} 4} \) в сумме образуют развёрнутый угол. Значит, \(\displaystyle \angle 1+ \angle {\color {red} 4}+\angle 3=180^{\circ} {\small.}\) |
По условию прямые \(\displaystyle m\) и \(\displaystyle n\) параллельны. \(\displaystyle \angle 2 \) и \(\displaystyle \angle {\color {red} 4}\) – накрест лежащие углы. Следовательно, \(\displaystyle \angle {\color {red} 4}=\angle 2 {\small.}\) Тогда \(\displaystyle \angle 1+\angle 2+ \angle 3=180^{\circ} {\small.}\) Получаем \(\displaystyle 66^{\circ}+88^{\circ}+ \angle 3=180^{\circ} {\small,}\) \(\displaystyle \angle 3=180^{\circ}-(66^{\circ}+88^{\circ})=180^{\circ}-154^{\circ}=26^{\circ} {\small.}\) | 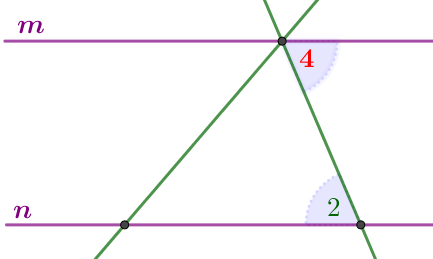 |
Ответ: \(\displaystyle 26{\small.}\)