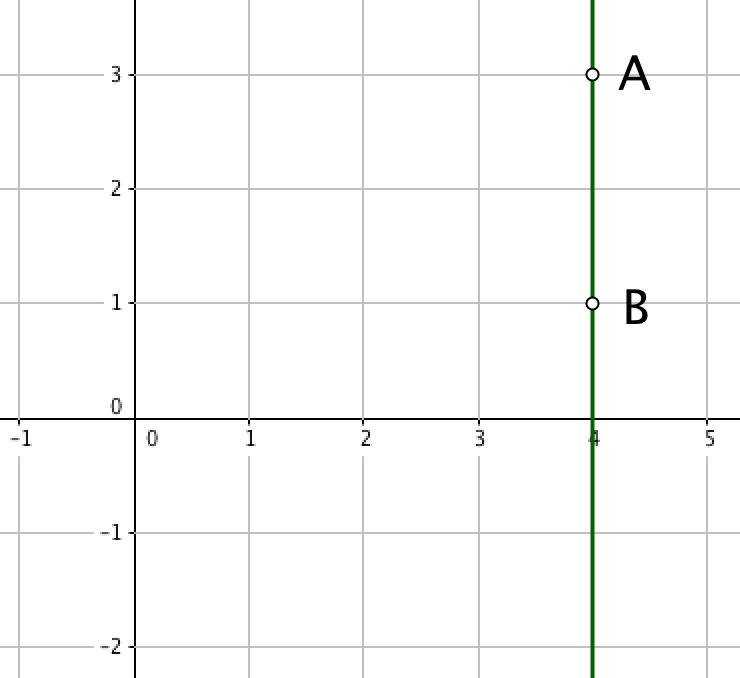
Найдите уравнение прямой, проходящей через точки \(\displaystyle A(4;3)\) и \(\displaystyle B(4;\, 1){\small :}\)
\(\displaystyle x=\)
Прямая задается:
- либо уравнением \(\displaystyle y=kx+b{\small ,}\) для некоторых чисел \(\displaystyle k,\, b\) (то есть является графиком линейной функции),
- либо уравнением \(\displaystyle x=a{\small ,}\) для некоторого числа \(\displaystyle a{\small .}\)
По рисунку видим, что данная прямая параллельна оси OY, и, значит, она задается уравнением \(\displaystyle x=a {\small . }\)
Для нахождения этого уравнения возьмем одну из точек на прямой, например, \(\displaystyle A(4;3){\small . }\)
Подставим ее координаты в в уравнение прямой \(\displaystyle x=a\,{\small . } \)
Точка \(\displaystyle A(\color{blue}{ 4};\color{green}{3}) \) имеет координаты \(\displaystyle x=\color{blue}{ 4}\) и \(\displaystyle y=\color{green}{ 3}{\small , }\) поэтому
\(\displaystyle \color{blue}{ 4}=a {\small , }\)
или
\(\displaystyle a=4{\small . } \)
Таким образом, уравнение прямой имеет вид:
\(\displaystyle x=4{\small . } \)
Ответ: \(\displaystyle x={\bf 4}{\small . } \)