Изображена некоторая прямая \(\displaystyle y=kx+b\,{\small : }\)
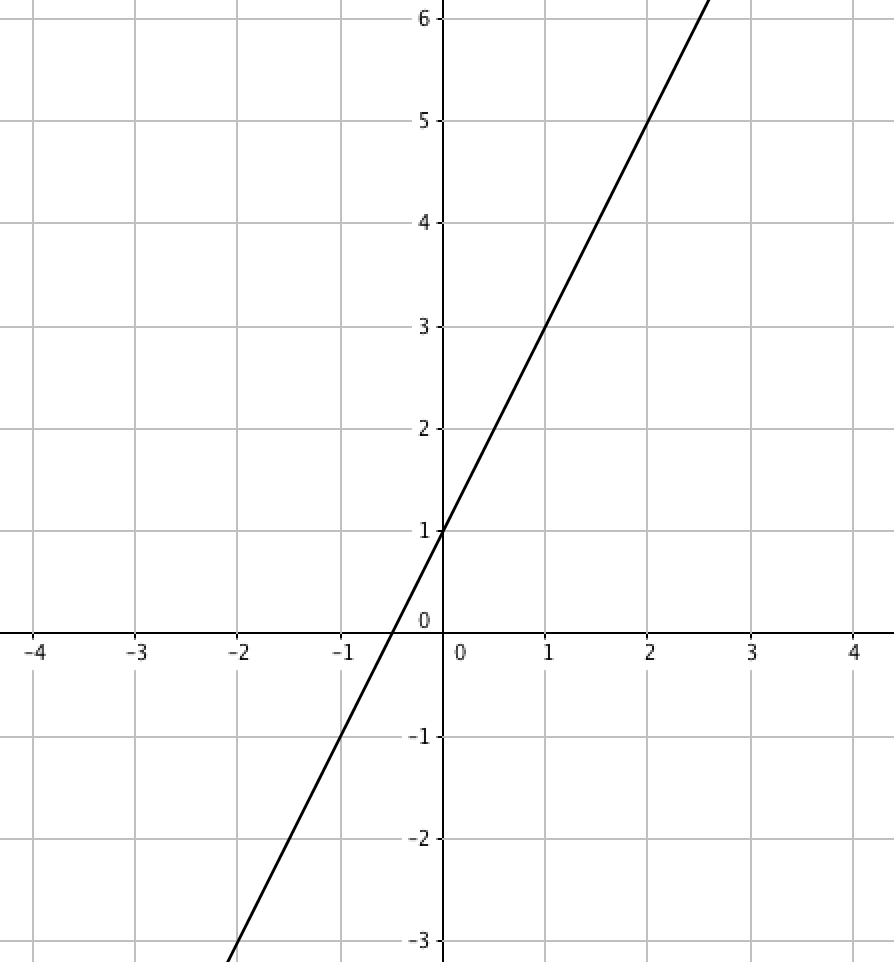
Запишите уравнения для коэффициентов \(\displaystyle k\) и \(\displaystyle b\) при подстановке координат точек этой прямой:
\(\displaystyle \left\{ \vphantom{\begin{aligned} 1\\[5px] 1 \end{aligned}} \right. \) | \(\displaystyle =k\,\cdot \)\(\displaystyle +b{\small ,}\) |
\(\displaystyle =k\,\cdot \)\(\displaystyle +b{\small .}\) |
На заданной прямой выберем две произвольные точки \(\displaystyle A\) и \(\displaystyle B{\small . }\)
Удобно выбрать точки с целыми координатами, например, такие как на рисунке:
Для получения правильного ответа могут быть выбраны любые точки, лежащие на заданной прямой.
Подставим координаты точек \(\displaystyle A \) и \(\displaystyle B \) в уравнение прямой \(\displaystyle y=kx+b\,{\small . } \)
Точка \(\displaystyle A(\color{blue}{ 1};\color{green}{3}) \) с координатами \(\displaystyle x=\color{blue}{ 1}\) и \(\displaystyle y=\color{green}{ 3}{\small , }\) поэтому
\(\displaystyle \color{green}{3}=k\cdot \color{blue}{ 1}+b \,{\small . }\)
Точка \(\displaystyle B(\color{blue}{ 2};\color{green}{ 5}) \) с координатами \(\displaystyle x=\color{blue}{ 2}\) и \(\displaystyle y=\color{green}{ 5}{\small , }\) поэтому
\(\displaystyle \color{green}{ 5}=k\cdot \color{blue}{ 2}+b {\small . }\)
Таким образом, уравнения для коэффициентов \(\displaystyle k \) и \(\displaystyle b \) будут иметь вид:
\(\displaystyle \left\{\begin{array}{rl}{\bf 3} &\kern{-1em}\,=k\cdot {\bf 1}+b {\small , }\\{\bf 5} &\kern{-1em}\,=k\cdot {\bf 2}+b {\small . }\end{array}\right.\)