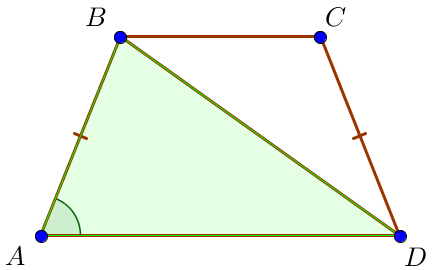
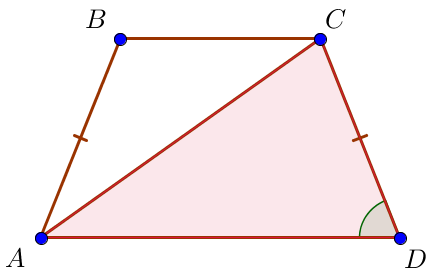
В равнобедренной трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AD\) и \(\displaystyle BC\) \(\displaystyle O\) – точка пересечения диагоналей, угол \(\displaystyle CAD\) равен \(\displaystyle 36^\circ \small.\) Чему равен угол \(\displaystyle AOD\ \small?\) Ответ дайте в градусах.
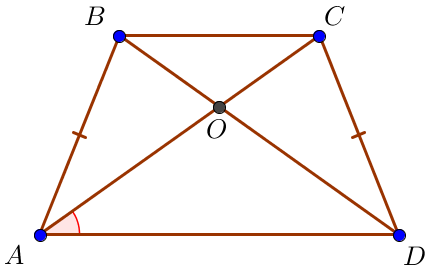
Рассмотрим треугольники \(\displaystyle ABD\) и \(\displaystyle ACD\small.\) Они равны по двум сторонам и углу между ними:
Значит, углы \(\displaystyle ADB\) и \(\displaystyle DAC\) равны.
Тогда \(\displaystyle \angle ADB=\angle CAD=36^{\circ}\small.\) |
|
Из треугольника \(\displaystyle AOD\) \(\displaystyle \angle AOD=180^{\circ} - \angle OAD - \angle ODA=\) \(\displaystyle =180^{\circ} - 36^{\circ} - 36^{\circ} = 108^{\circ}\small. \) | 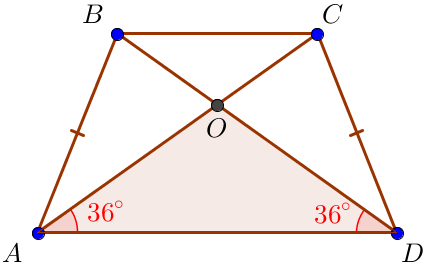 |
Ответ: \(\displaystyle 108^{\circ}{\small .}\)