На рисунке изображены четыре прямые: \(\displaystyle a{\small ,}\) \(\displaystyle b{\small ,}\) \(\displaystyle c\) и \(\displaystyle d{\small .}\) Какая из них является графиком линейной функции \(\displaystyle y=-2x+6{\small ? }\)
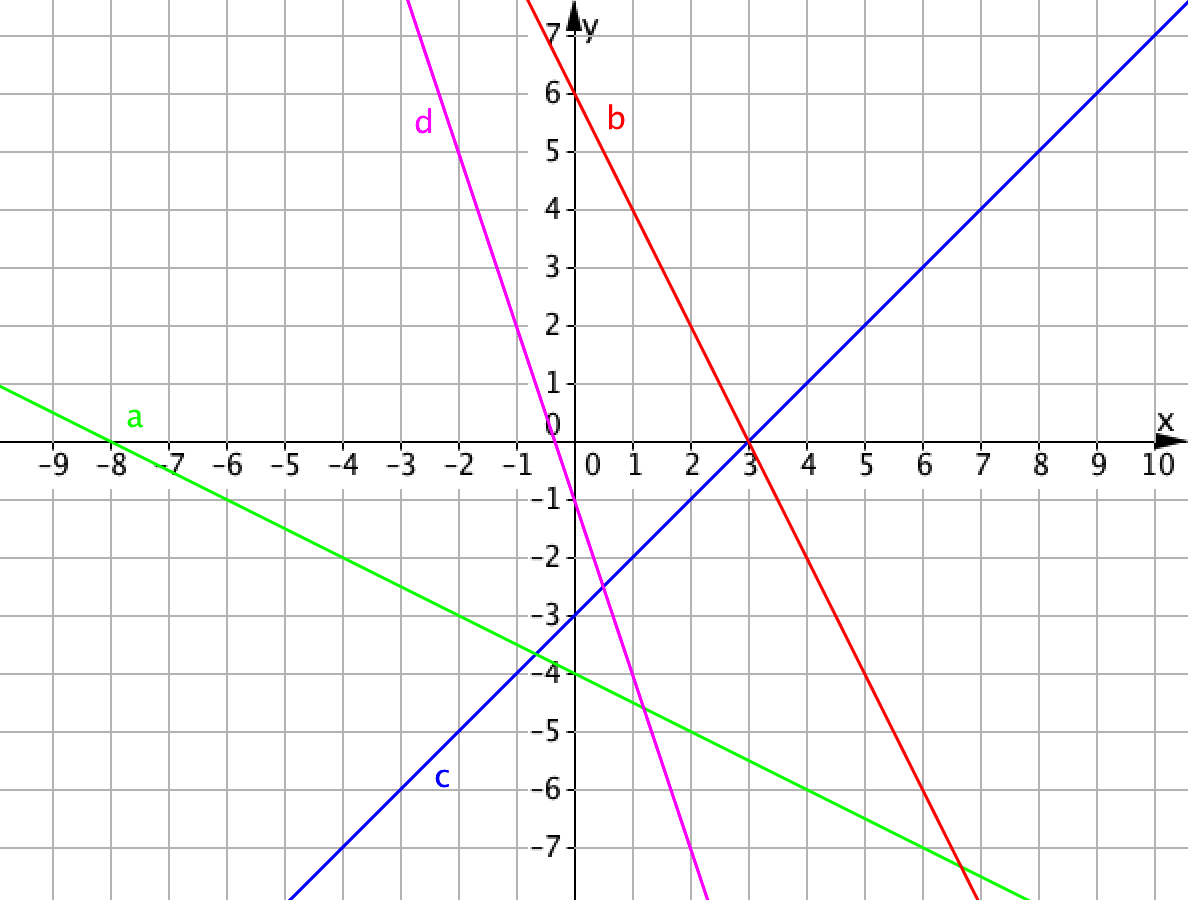
Напомним, что если прямая является графиком линейной функции \(\displaystyle y=-2x+6\) и проходит через некоторую точку, то эта точка будет удовлетворять уравнению \(\displaystyle y=-2x+6{\small . }\)
Будем по порядку брать произвольные точки, через которые проходят прямые, и проверять, удовлетворяют ли эти точки уравнению \(\displaystyle y=-2x+6{\small : }\)
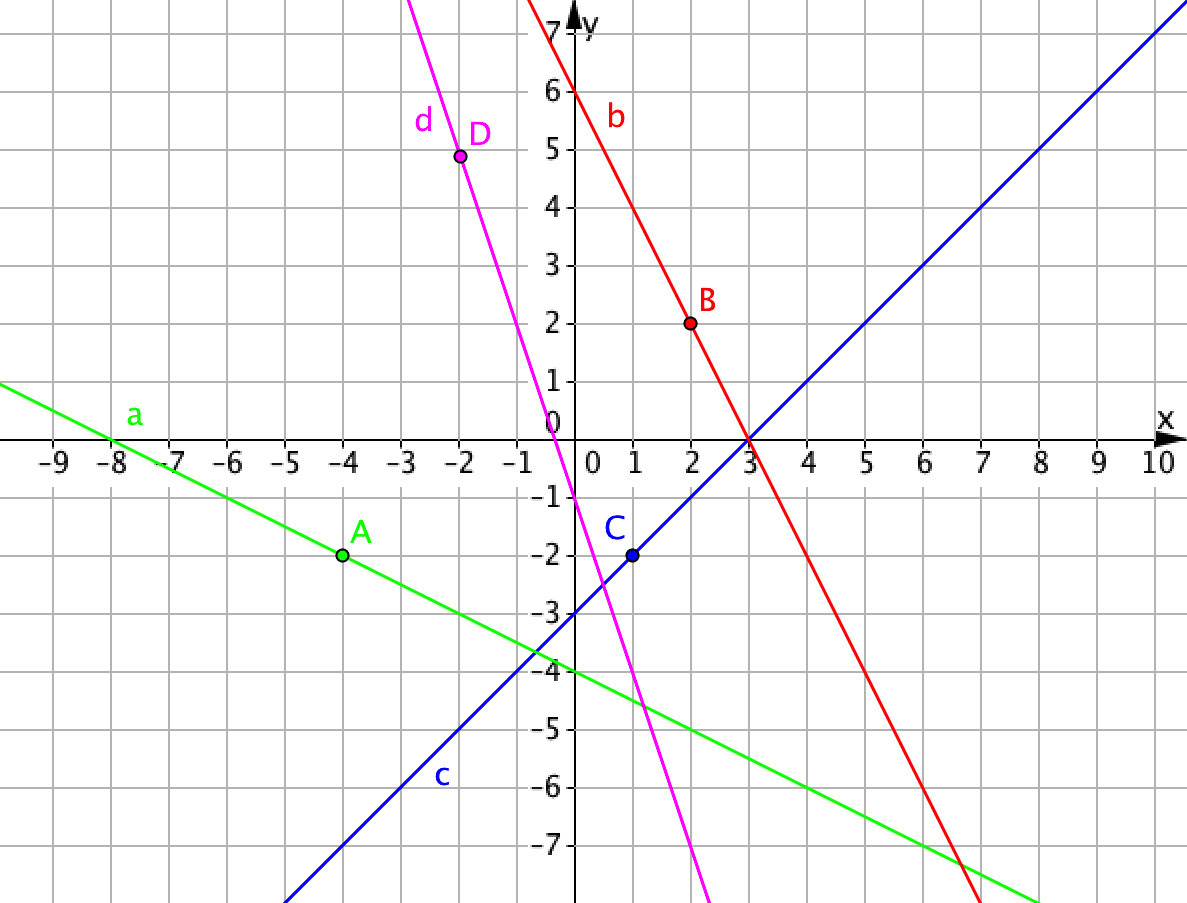
| Прямая | Точка прямой | Функция \(\displaystyle y=-2x+6\) | Результат |
| \(\displaystyle a \) | \(\displaystyle (\color{blue}{-4};\color{green}{-2}) \) | \(\displaystyle \color{green}{-2}=-2\cdot (\color{blue}{-4})+6;\) \(\displaystyle -2=14\) | неверно |
| \(\displaystyle b \) | \(\displaystyle (\color{blue}{2};\color{green}{2}) \) | \(\displaystyle \color{green}{2}=-2\cdot \color{blue}{2}+6;\) \(\displaystyle 2=2\) | верно |
| \(\displaystyle c \) | \(\displaystyle (\color{blue}{1};\color{green}{-2}) \) | \(\displaystyle \color{green}{-2}=-2\cdot \color{blue}{1}+6\) \(\displaystyle -2=4\) | неверно |
| \(\displaystyle d \) | \(\displaystyle (\color{blue}{-2};\color{green}{5}) \) | \(\displaystyle \color{green}{5}=-2\cdot (\color{blue}{-2})+6\) \(\displaystyle 5=10\) | неверно |
Значит, только точка прямой \(\displaystyle b\) удовлетворяет уравнению \(\displaystyle y=-2x+6{\small ,}\) и, следовательно, эта прямая является графиком этой функции.
Ответ: прямая \(\displaystyle b{\small .} \)