Луч \(\displaystyle OC\) делит развернутый угол \(\displaystyle ∠ AOB\) на два смежных угла \(\displaystyle ∠ AOC\) и \(\displaystyle ∠ BOC\) так, что угол \(\displaystyle ∠ AOC\) на \(\displaystyle 30^{\circ}\) больше угла \(\displaystyle ∠ BOC\). Чему равны углы \(\displaystyle ∠ AOC\) и \(\displaystyle ∠ BOC\)?
Развернутые и смежные углы
Если на прямой отметить точку, то образуются два луча, выходящих из этой точки. Эти лучи делят плоскость на две части, каждую из которых называют развернутым углом. На рисунке изображен развернутый угол \(\displaystyle ∠ ABC\).
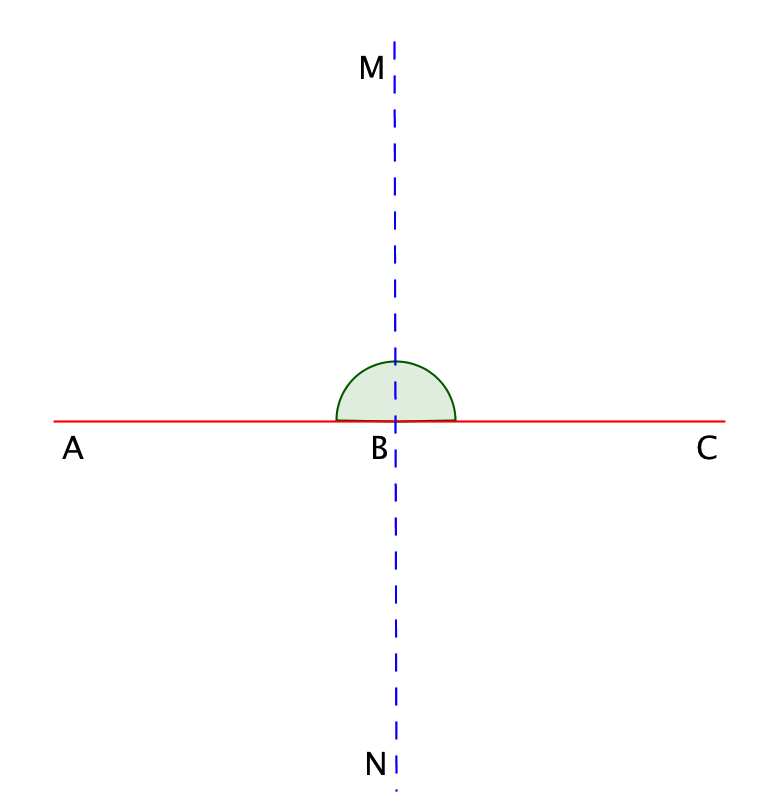
Развернутый угол составляет \(\displaystyle 180\) градусов: \(\displaystyle ∠ ABC=180^{\circ}\).
Внутри развернутого угла \(\displaystyle ∠ ABC\) проведен луч \(\displaystyle BD\). Он разбивает развернутый угол на два угла: \(\displaystyle ∠ ABD\) и \(\displaystyle ∠ DBC\), которые называются смежными углами.
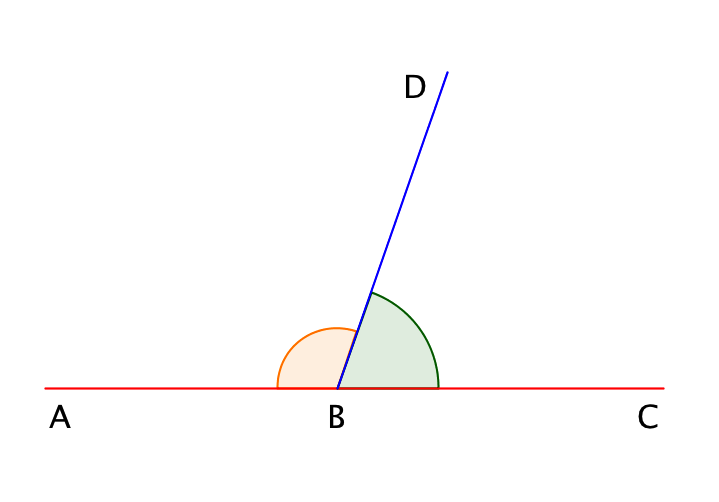
Сумма смежных углов равна \(\displaystyle 180^{\circ}\):
\(\displaystyle ∠ ABD+∠ DBC=∠ ABС=180^{\circ}.\)
Поскольку углы \(\displaystyle ∠ AOC\) и \(\displaystyle ∠ BOC\) – смежные, то их сумма равна \(\displaystyle 180^{\circ}\):
\(\displaystyle ∠ AOC+∠ BOC=180^{\circ}\).
Пусть \(\displaystyle x\) – величина угла \(\displaystyle ∠ BOC\), тогда \(\displaystyle x+30^{\circ}\) – величина угла \(\displaystyle ∠ AOC\).
Таким образом,
\(\displaystyle x+x+30^{\circ}=180^{\circ}\).
\(\displaystyle 2\cdot x=150^{\circ}\)
\(\displaystyle x=75^{\circ}\).
Следовательно, \(\displaystyle ∠ BOC=75^{\circ}\), \(\displaystyle ∠ AOC=75^{\circ}+30^{\circ}=105^{\circ}\).
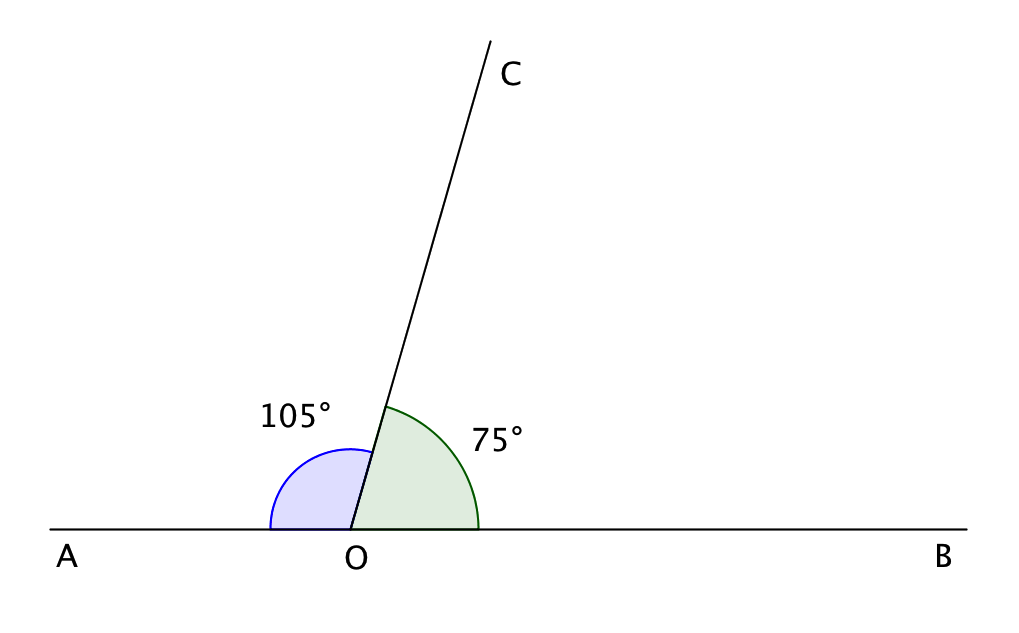
Ответ: \(\displaystyle ∠ AOC=105^{\circ}\), \(\displaystyle ∠ BOC=75^{\circ}\).