Какой из углов, показанных на рисунке, является развернутым?

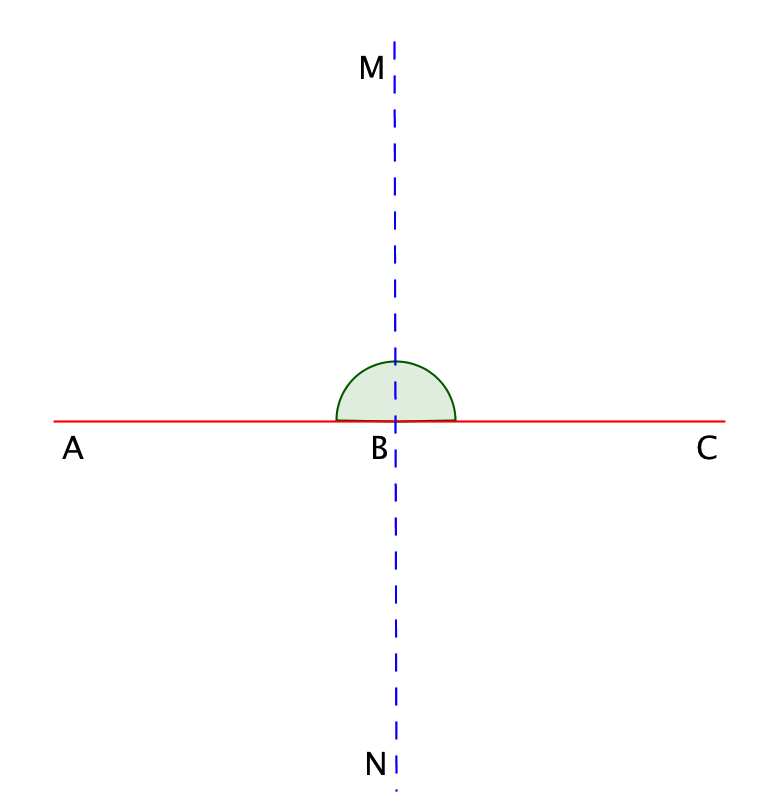
Если на прямой отметить точку, то образуются два луча, выходящих из этой точки. Эти лучи делят плоскость на две части, каждую из которых называют развернутым углом. На рисунке изображен развернутый угол \(\displaystyle ∠ ABC\).
Развернутый угол составляет \(\displaystyle 180\) градусов: \(\displaystyle ∠ ABC=180^{\circ}\).
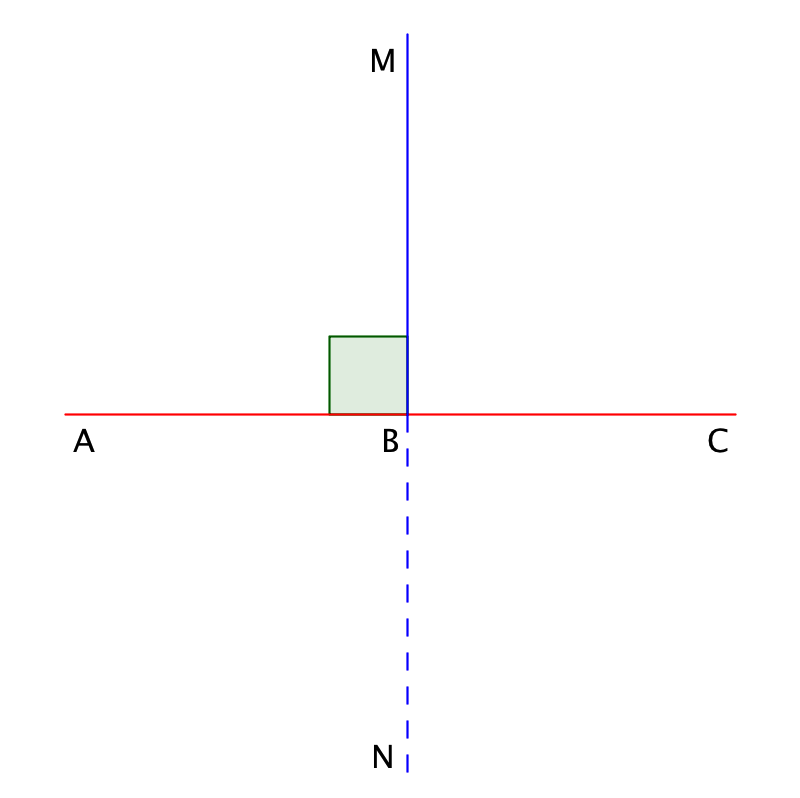
Перевернем лист бумаги так, чтобы лучи \(\displaystyle BA\) и \(\displaystyle BC\) совпали, и расправим лист. Тогда линия сгиба \(\displaystyle MN\) делит каждый из развернутых углов на два равных угла, каждый из которых называют прямым углом.
Прямой угол - половина развернутого угла. Он составляет \(\displaystyle 90\) градусов: \(\displaystyle ∠ ABM=90^{\circ}\).
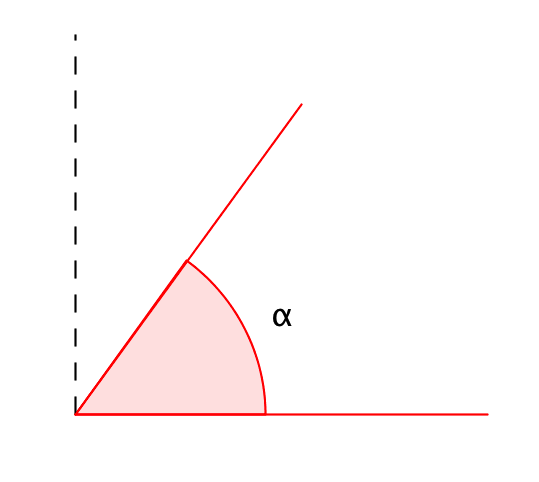
Если угол \(\displaystyle \alpha\) меньше прямого, то его называют острым: \(\displaystyle \alpha<90^{\circ}\).
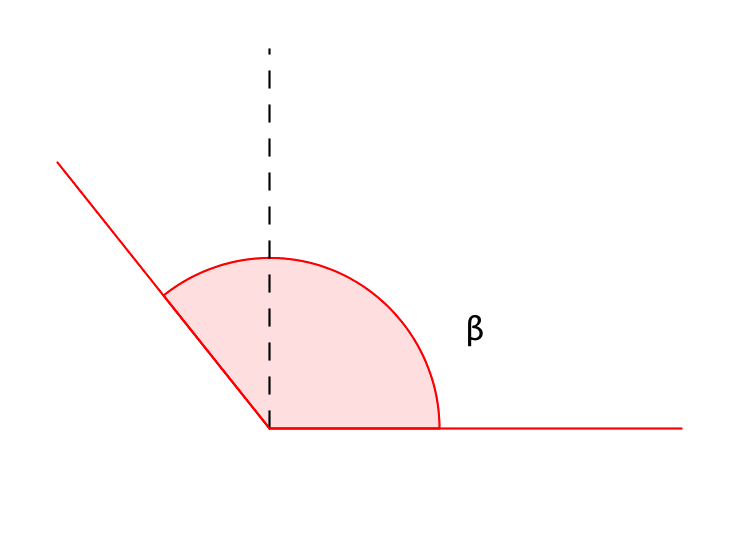
Если угол \(\displaystyle \beta\) больше прямого, но меньше развернутого, то его называют тупым: \(\displaystyle 90^{\circ}<\beta<180^{\circ}\).
Углы: развернутый, прямой, острый, тупой
В нашем случае развернутым является угол \(\displaystyle ∠ ACD\) – он делит всю плоскость на две части, и его величина составляет \(\displaystyle 180^{\circ}\).

Ответ: \(\displaystyle ∠ ACD\).