На какой угол повернется минутная стрелка через \(\displaystyle 5\) минут?
Угол отсчитывать от конечного положения минутной стрелки против хода часов.
\(\displaystyle \alpha=\) \(\displaystyle ^{\circ}\)
Полный оборот стрелки часов соответствует углу в \(\displaystyle 360^{\circ}\).
Пусть первоначально минутная стрелка была направлена вверх, что, например, соответствует времени \(\displaystyle 3{:}00\) часа:
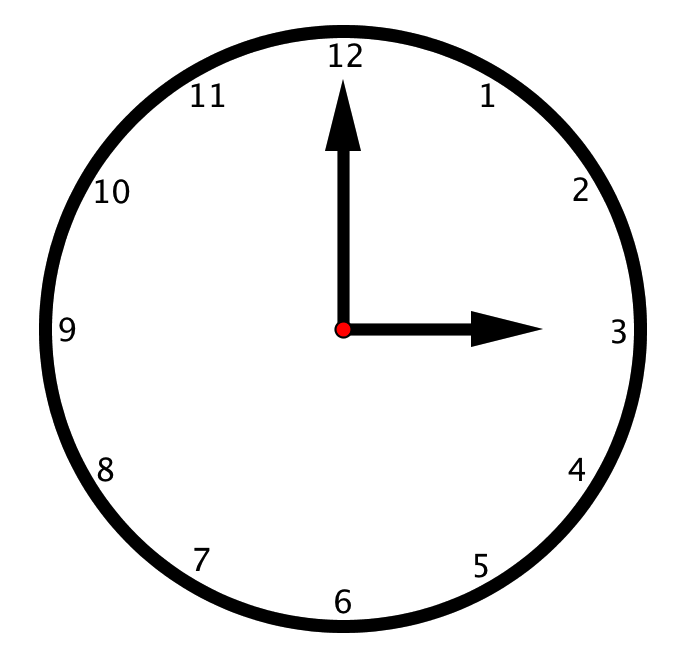
Через \(\displaystyle 5\) минут минутная стрелка часов совершит \(\displaystyle \frac{1}{12}\) оборота. Таким образом, часы покажут время \(\displaystyle 3{:}05\):
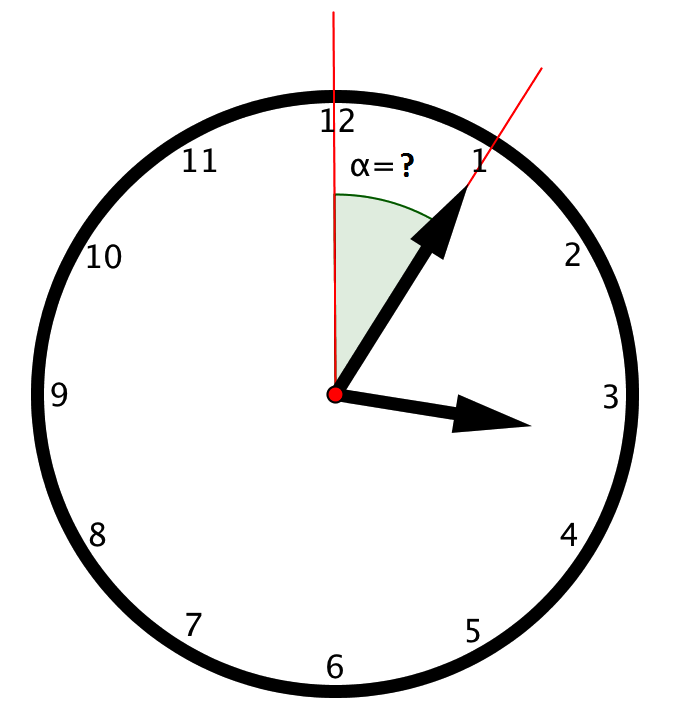
Следовательно, конец минутной стрелки за \(\displaystyle 5\) минут опишет дугу, равную \(\displaystyle \frac{1}{12}\) длины окружности, а сама минутная стрелка повернется на угол \(\displaystyle \alpha\), равный \(\displaystyle \frac{1}{12}\) угла в \(\displaystyle 360^{\circ}\), то есть на угол
\(\displaystyle \alpha=\frac{1}{12}\cdot 360=\frac{360}{12}=30^{\circ}\).
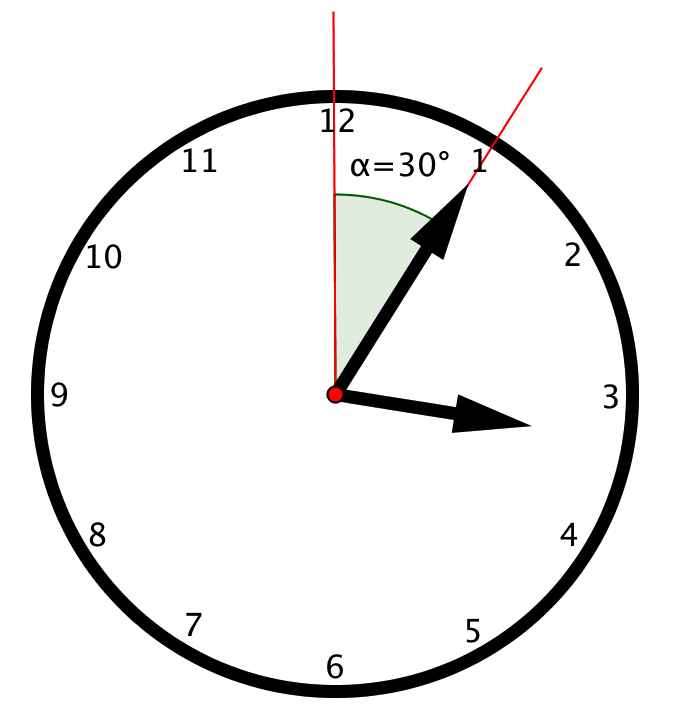
Ответ: \(\displaystyle \alpha=30^{\circ}\).