Чему равно расстояние между точками \(\displaystyle A\) и \(\displaystyle B\), изображенными на координатном луче?
Координата любой точки на луче равна расстоянию от точки \(\displaystyle O(0)\) до данной точки, то есть сумме длин единичных отрезков, укладывающихся на этом расстоянии.
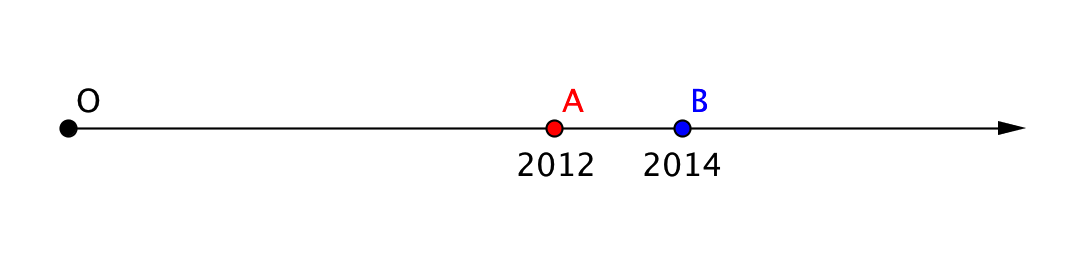
Изобразим на координатном луче точки \(\displaystyle A(2012)\) и \(\displaystyle B(2014)\). Поскольку координаты этих точек велики по сравнению с координатой конца единичного отрезка (равной \(\displaystyle 1\)), то сам единичный отрезок указывать на рисунке не будем. Кроме того, нас интересует лишь взаимное расоложение точек \(\displaystyle A\) и \(\displaystyle B\), поэтому не будем придерживаться масштаба:
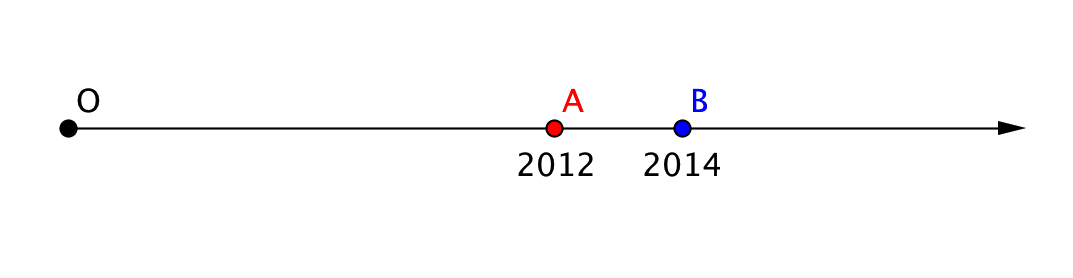
Как видно из рисунка, расстояние от точки \(\displaystyle O\) до точки \(\displaystyle A\) равно сумме длин \(\displaystyle 2012\)-ти единичных отрезков. Таким образом, координата точки \(\displaystyle A\) равна \(\displaystyle 2012\) и обозначается \(\displaystyle A(2012)\).
Расстояние от точки \(\displaystyle O\) до точки \(\displaystyle B\) равно сумме длин \(\displaystyle 2014\)-ти единичных отрезков. Следовательно, координата точки \(\displaystyle B\) равна \(\displaystyle 2014\) и обозначается \(\displaystyle B(2014)\).
Таким образом, расстояние между точками \(\displaystyle A(2012)\) и \(\displaystyle B(2014)\) равно длине отрезка \(\displaystyle AB\), или разности координат его правого и левого концов, – то есть соответственно координат точек \(\displaystyle A(2012)\) и \(\displaystyle B(2014)\):
\(\displaystyle AB=OB-OA=2014-2012=2\).
Ответ: \(\displaystyle 2\).