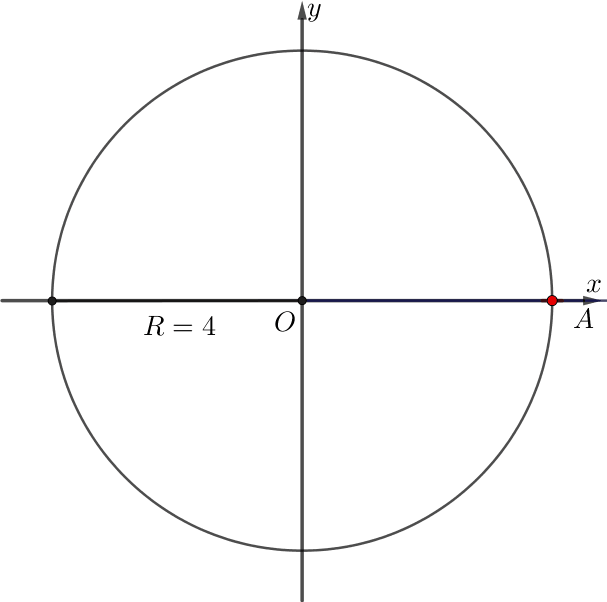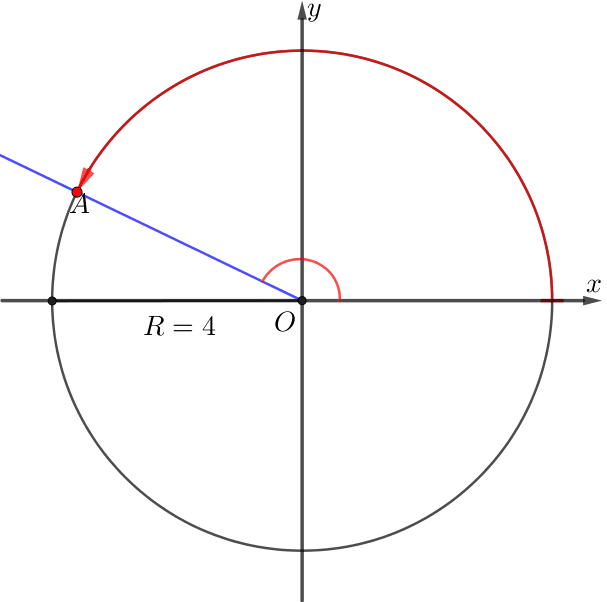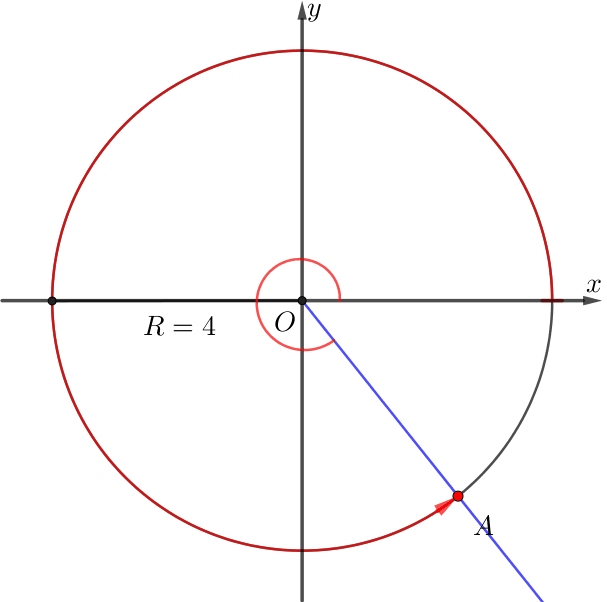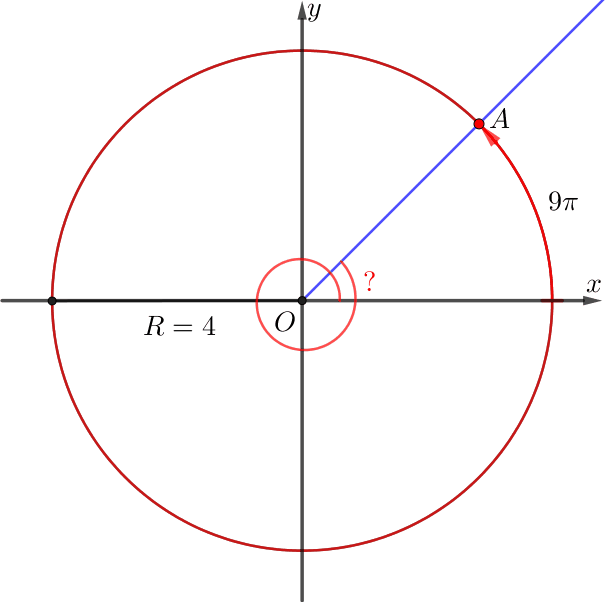
Луч \(\displaystyle OA\) повернулся на угол \(\displaystyle \alpha{\small.}\) Точка \(\displaystyle A\) все время двигалась по окружности радиуса \(\displaystyle R=4{\small.}\) Чему равен \(\displaystyle \alpha\) в радианах, если длина пути, пройденного точкой \(\displaystyle A{\small ,}\) равна \(\displaystyle 9\pi{\small?}\)
Центральный угол в один радиан опирается на дугу, длина которой равна радиусу \(\displaystyle R{\small:} \)
Тогда при повороте луча на \(\displaystyle 1\) радиан точка \(\displaystyle A{\small,}\) двигаясь по окружности радиуса \(\displaystyle R{\small,}\)проходит расстояние \(\displaystyle R{\small.}\)
Значит, при повороте луча на \(\displaystyle \alpha\) радиан:
расстояние, пройденное точкой \(\displaystyle A{\small,}\) равно \(\displaystyle \alpha\cdot R{\small.}\)
По условию, расстояние, пройденное точкой \(\displaystyle A{\small,}\) равно \(\displaystyle 9\pi\) и \(\displaystyle R=4{\small.}\)
Значит,
\(\displaystyle 9\pi=\alpha\cdot 4{\small.}\)
Откуда находим \(\displaystyle \alpha{\small:}\)
\(\displaystyle \alpha=\frac{9\pi}{4}{\small.}\)
Ответ: \(\displaystyle \frac{9\pi}{4}\) радиан.