\(\displaystyle \cos(t)=0{,}63,\,\sin(t)=-0{,}77{\small }\)
болатындай \(\displaystyle t\) бұрышының жықын мәнін табыңыз.
\(\displaystyle t \approx \) радиан.
Центрі \(\displaystyle O\) нүктесі болатын бірлік шеңбер берілген. \(\displaystyle A\) нүктесінің координатасы \(\displaystyle (1;0){\small .}\)
\(\displaystyle OA\) сәулесі \(\displaystyle \color{red}{\alpha}{\small}\) бұрышына бұрылды.
Сонда
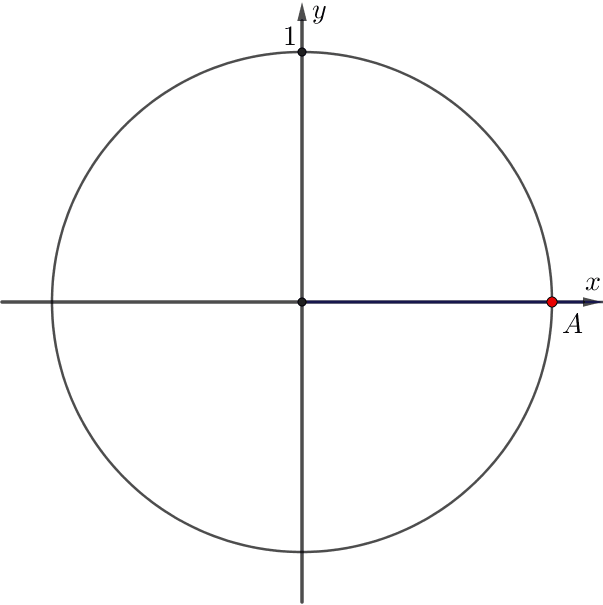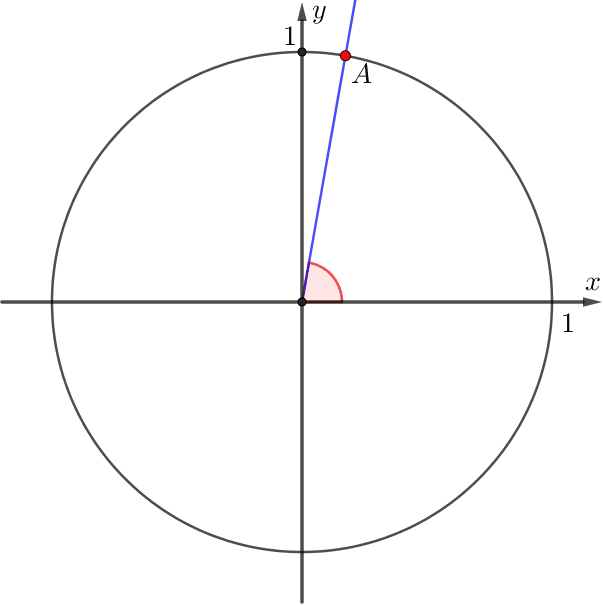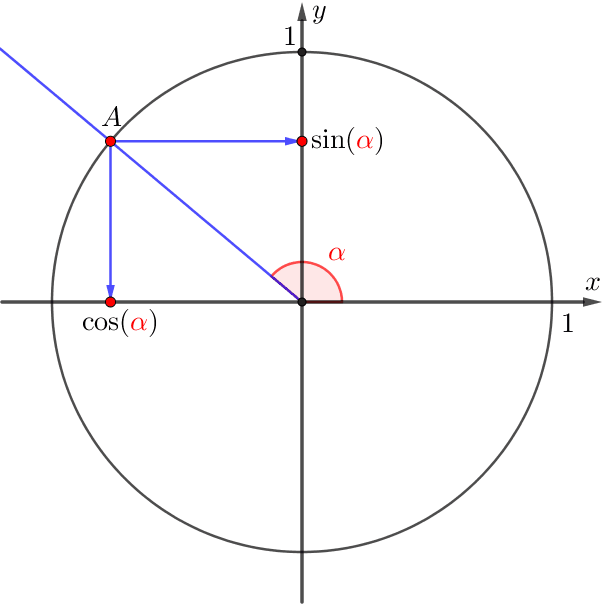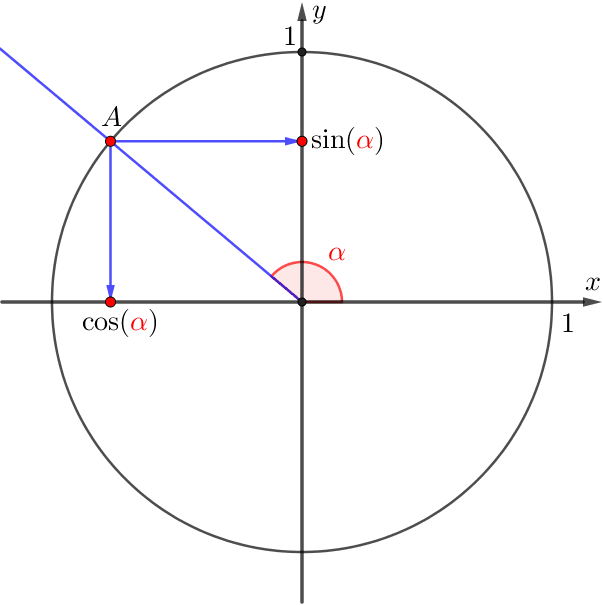
- \(\displaystyle \color{red}{\alpha}\) бұрышының косинусы деп \(\displaystyle A\) нүктесінің абсциссасын айтамыз және \(\displaystyle \cos(\color{red}{\alpha}){\small}\) деп белгіленеді,
- \(\displaystyle \color{red}{\alpha}\) бұрышының синусы деп \(\displaystyle A\) нүктесінің ординатасын айтамыз және \(\displaystyle \sin(\color{red}{\alpha}){\small}\) деп белгіленеді.
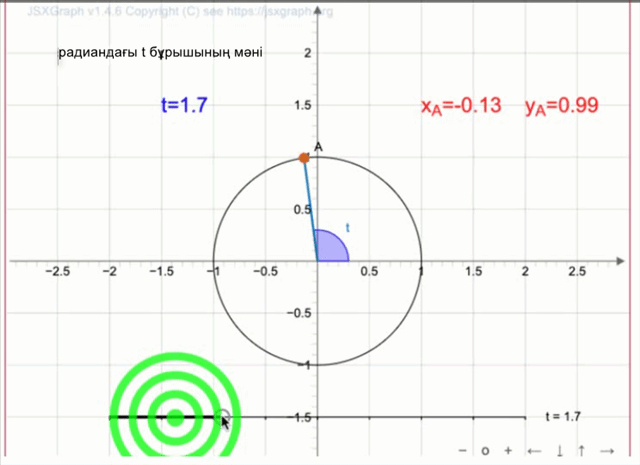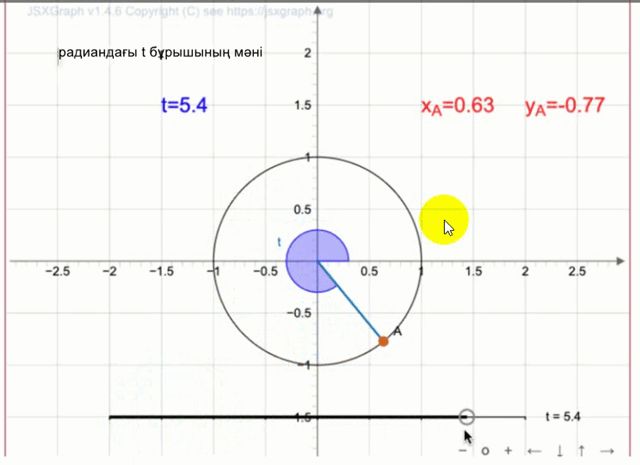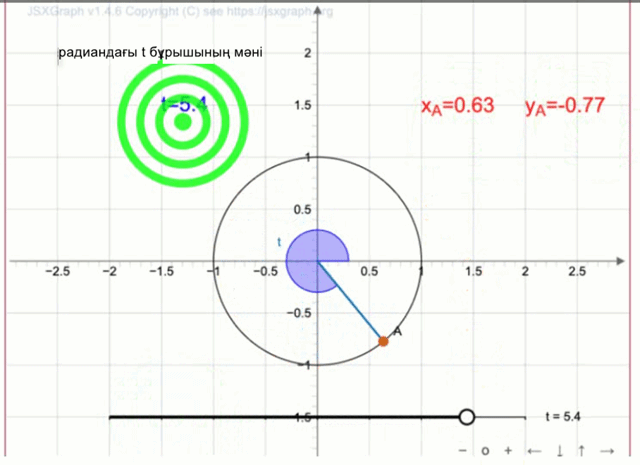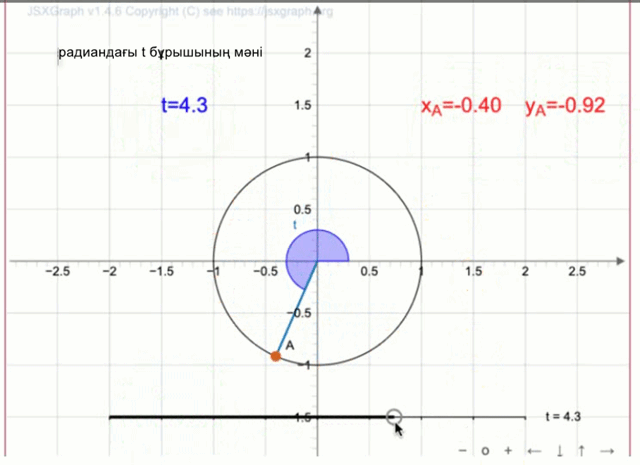
\(\displaystyle t\) параметрін \(\displaystyle A\) нүктесінің координатасы \(\displaystyle (0{,}63;\, -0{,}77){\small}\) болатындай етіп орналастырамыз.
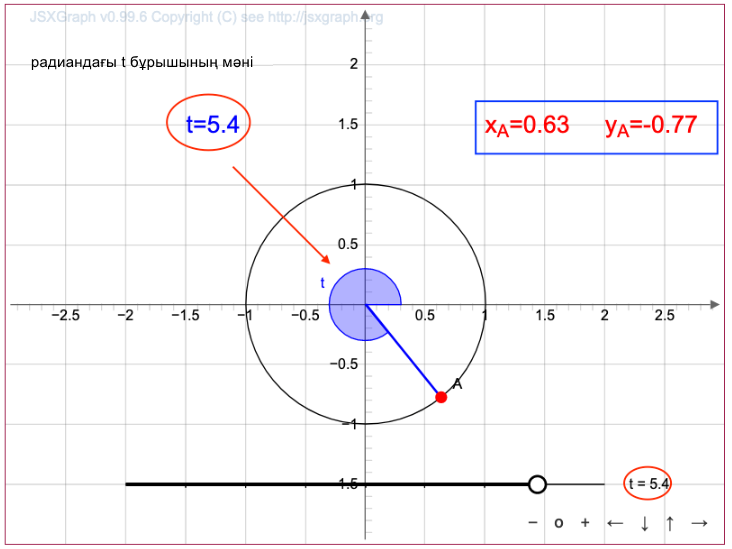
Графикте \(\displaystyle t\) бұрышының мәні \(\displaystyle t \approx 5{,}4\) радианға жуық екені көрсетілген.
Жауабы:\(\displaystyle 5{,}4\) радиан.