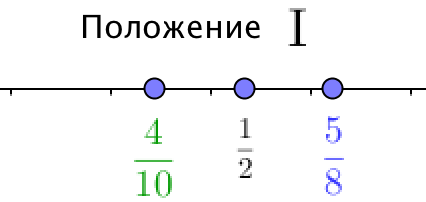
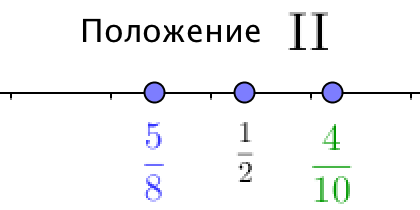
Выберите правильное расположение точек на прямой:
|
|
и сравните дроби
\(\displaystyle \frac{5}{8}\)\(\displaystyle \frac{4}{10}\)
Посмотрим на рисунки:
|
|
На них видно, что нам необходимо сравнить числа \(\displaystyle \frac{ 4}{ 10},\,\,\frac{ 1}{ 2} \) и \(\displaystyle \frac{ 5}{ 8}{\small . } \)
Заметим, что дробь меньше \(\displaystyle \frac{ 1}{ 2}{\small , } \) если ее числитель меньше половины знаменателя.
И, наоборот, дробь больше \(\displaystyle \frac{ 1}{ 2}{\small , } \) если ее числитель больше половины знаменателя.
Поскольку для дроби \(\displaystyle \frac{4}{10}\) числитель \(\displaystyle 4 \) меньше половины знаменателя (то есть \(\displaystyle 4<\frac{ 10}{ 2}=5\)), то \(\displaystyle \frac{4}{10}<\frac{ 1}{ 2}{\small . }\)
Точно так же, так как для дроби \(\displaystyle \frac{5}{8}\) числитель \(\displaystyle 5\) больше половины знаменателя (то есть \(\displaystyle 5>\frac{ 8}{ 2}=4\)), то \(\displaystyle \frac{5}{8}>\frac{ 1}{ 2}{\small . }\)
Мы получили, что \(\displaystyle \frac{4}{10}<\color{green}{ \frac{ 1}{ 2}}\) и \(\displaystyle \color{green}{ \frac{ 1}{ 2}}<\frac{5}{8}{\small . }\) Значит, \(\displaystyle \frac{4}{10}<\color{green}{ \frac{ 1}{ 2}}<\frac{5}{8}{\small . }\)
Из этого неравенства и получаем расположение чисел на числовой оси слева направо: \(\displaystyle \frac{4}{10}{\small , }\,\,\frac{ 1}{ 2} \) и \(\displaystyle \frac{ 5}{ 8}{\small . } \)
Таким образом, верным является положение \(\displaystyle \text{I}{\small . }\)
Ответ: положение \(\displaystyle \text{I} \) и \(\displaystyle \frac{5}{8} > \frac{4}{10} {\small . }\)