Сравните числа \(\displaystyle 3{,}579, \, \frac{11}{3}\) и \(\displaystyle \frac{15}{4}{\small ,}\) если известно положение точек на координатной прямой:
Нам нужно сравнить числа \(\displaystyle 3{,}579, \, \frac{11}{3}\) и \(\displaystyle \frac{15}{4}{\small .}\)
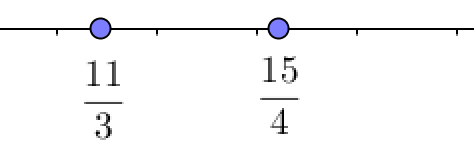
Посмотрим на первый рисунок:

На нем \(\displaystyle \frac{ 11}{ 3} \) располагается левее \(\displaystyle \frac{ 15}{ 4}{\small . } \) Значит, \(\displaystyle \frac{ 11}{ 3}< \frac{ 15}{ 4}{\small . } \)
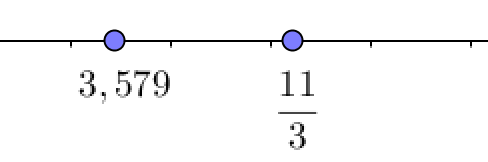
Теперь посмотрим на второй рисунок:

На нем \(\displaystyle 3{,}579 \) располагается левее \(\displaystyle \frac{ 11}{ 3}{\small . } \) Значит, \(\displaystyle 3{,}579<\frac{ 11}{ 3}{\small . } \)
Получаем, что \(\displaystyle \frac{ 11}{ 3}< \frac{ 15}{ 4} \) и \(\displaystyle 3{,}579<\frac{ 11}{ 3}{\small . } \) Следовательно,
\(\displaystyle 3{,}579<\frac{ 11}{3}< \frac{ 15}{ 4}{\small . } \)
Ответ: \(\displaystyle 3{,}579<\frac{ 11}{3}< \frac{ 15}{ 4}{\small . } \)