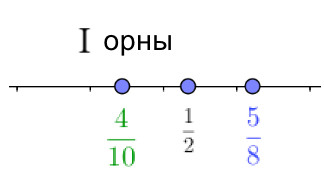
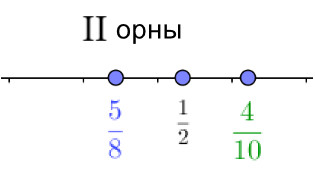
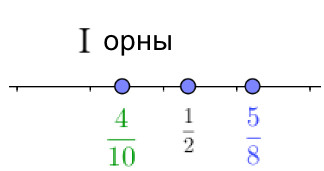
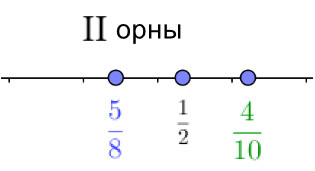
Түзудегі нүктелердің дұрыс орналасуын таңдаңыз:
|
|
және
\(\displaystyle \frac{5}{8}\)\(\displaystyle \frac{4}{10}\) бөлшектерін салыстырыңыз
Суреттерді қарастырайық:
|
|
Онда бізге \(\displaystyle \frac{ 4}{ 10},\,\,\frac{ 1}{ 2} \) және \(\displaystyle \frac{ 5}{ 8}{\small } \) сандарын салыстыру қажет екендігі көрінеді.
Бөлшек егер оның алымы бөлімінің жартысынан аз болса, \(\displaystyle \frac{ 1}{ 2}{\small } \)-ден кем болатынын ескерейік.
Және, керісінше, бөлшек егер оның алымы бөлімінің жартысынан көп болса, \(\displaystyle \frac{ 1}{ 2}{\small } \)-ден артық болады.
Себебі \(\displaystyle \frac{4}{10}\) бөлшегі үшін алымы \(\displaystyle 4 \) бөлімінің жартысынан аз болғандықтан (яғни \(\displaystyle 4<\frac{ 10}{ 2}=5\)), онда \(\displaystyle \frac{4}{10}<\frac{ 1}{ 2}{\small . }\)
Сол сияқты, \(\displaystyle \frac{5}{8}\) бөлшегі үшін алымы \(\displaystyle 5\) бөлімінің жартысынан көп болғандықтан (яғни \(\displaystyle 5>\frac{ 8}{ 2}=4\)), онда \(\displaystyle \frac{5}{8}>\frac{ 1}{ 2}{\small . }\)
Біз \(\displaystyle \frac{4}{10}<\color{green}{ \frac{ 1}{ 2}}\) және \(\displaystyle \color{green}{ \frac{ 1}{ 2}}<\frac{5}{8}{\small }\) алдық. Яғни, \(\displaystyle \frac{4}{10}<\color{green}{ \frac{ 1}{ 2}}<\frac{5}{8}{\small . }\)
Осы теңсіздіктен сандардың солдан оңға қарай сандық осьтегі орналасуын аламыз: \(\displaystyle \frac{4}{10}{\small , }\,\,\frac{ 1}{ 2} \) және \(\displaystyle \frac{ 5}{ 8}{\small . } \)
Осылайша, \(\displaystyle \text{I}{\small }\) орны дұрыс болып табылады.
Жауабы: \(\displaystyle \text{I} \) орны және \(\displaystyle \frac{5}{8} > \frac{4}{10} {\small . }\)