Найдите \(\displaystyle 9\tg(3\pi - \alpha),\) если \(\displaystyle \cos \alpha = -\frac{4}{5} \) и \(\displaystyle \alpha \in \left( \frac{\pi}{2};\ \pi \right) {\small.}\)
\(\displaystyle 9\tg(3\pi - \alpha)=\)
Применим формулу приведения.
Определим, в какой четверти находится угол \(\displaystyle 3\pi-\alpha \) (считая, что \(\displaystyle 0<\alpha<\frac{\pi}{2} \) ):
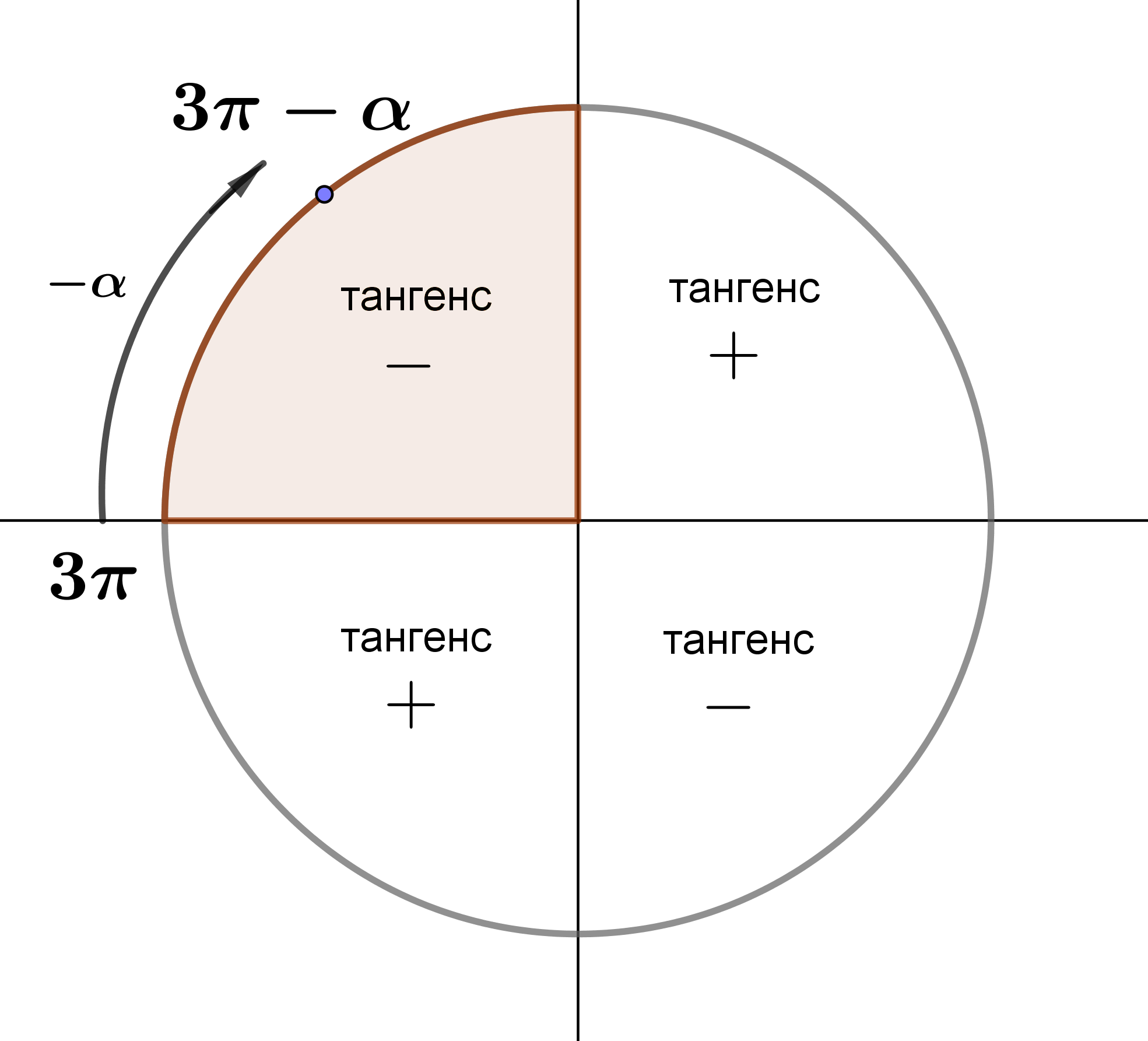
Во второй четверти тангенс отрицательный.
Так как первое слагаемое имеет вид \(\displaystyle \pi k ,\) где \(\displaystyle k\) – целое, то функция не меняется.
Значит,
\(\displaystyle 9\tg (3\pi-\alpha)=9(-\tg \alpha)=-9\tg \alpha{\small.}\)
Найдем \(\displaystyle \tg\alpha\) по формуле
\(\displaystyle \tg\alpha=\frac{\sin\alpha}{\cos \alpha}\)
По условию \(\displaystyle \cos \alpha = -\frac{4}{5} \).
Найдем \(\displaystyle \sin\alpha{\small .} \)
Вспомним основное тригонометрическое тождество.
\(\displaystyle \cos^2\alpha+\sin^2 \alpha=1\)
Отсюда получаем, что
\(\displaystyle \sin^2\alpha=1-\cos^2\alpha{\small.}\)
Подставим данное в условии значение \(\displaystyle \cos \alpha = -\frac{4}{5} {:}\)
\(\displaystyle \sin^2\alpha=1-\bigg(-\frac{4}{5}\bigg)^2=1-\frac{16}{25}=\frac{9}{25}{\small.}\)
Если \(\displaystyle \sin^2\alpha=\frac{9}{25}{ \small ,}\) то
\(\displaystyle \sin\alpha=\pm \sqrt{\frac{9}{25}},\)
\(\displaystyle \sin\alpha=\pm \frac{3}{5}{\small.}\)
Определим, какой именно знак имеет \(\displaystyle \sin\alpha{\small.}\)
По условию \(\displaystyle \alpha \in \left( \frac{\pi}{2};\ \pi \right){\small.}\)
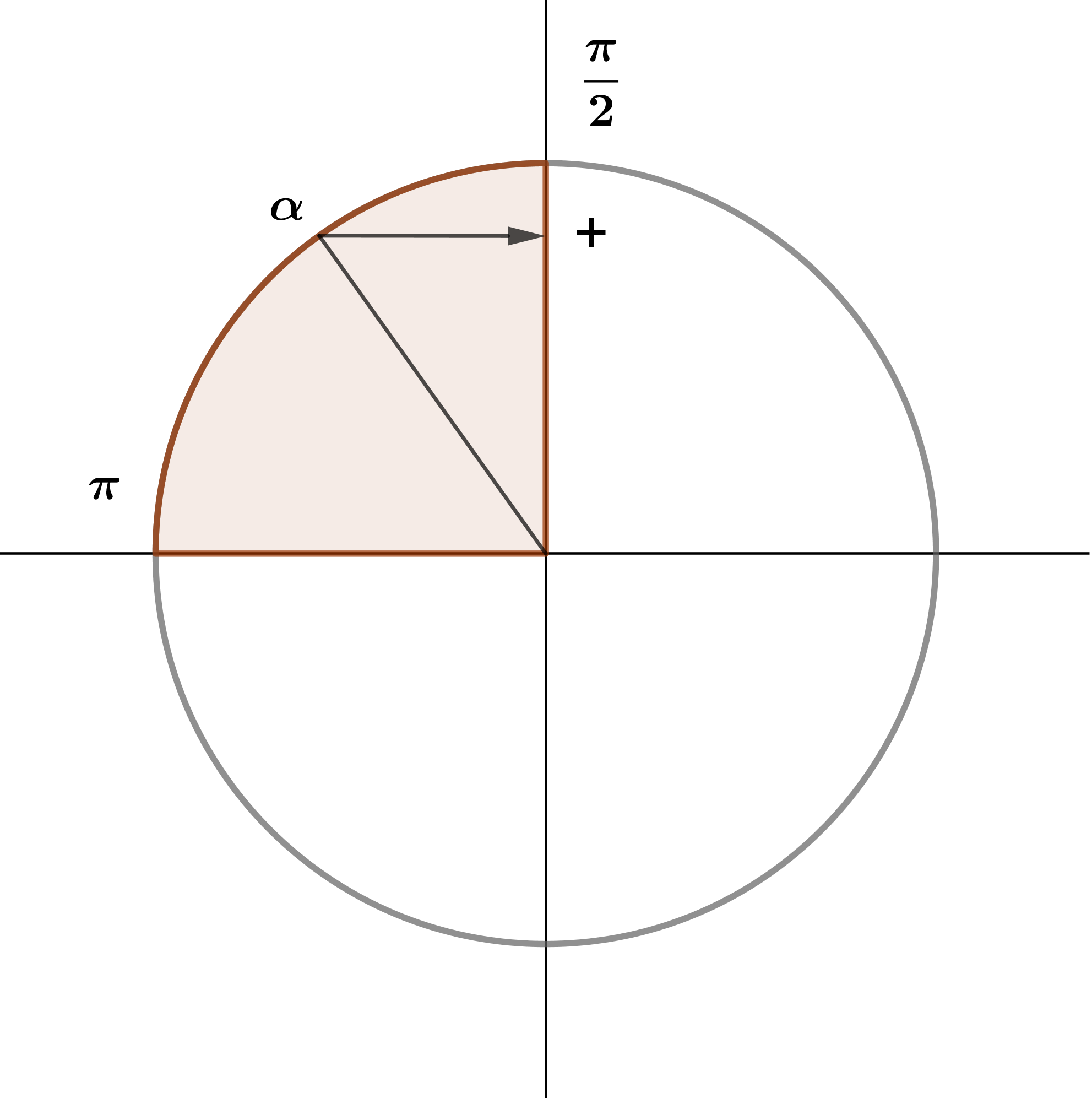
Во второй четверти значение синуса положительно. Следовательно,
\(\displaystyle \sin\alpha=\frac{3}{5}{\small.}\)
Тогда:
\(\displaystyle \tg\alpha=\frac{\sin\alpha}{\cos \alpha}=\frac{\frac{3}{5}}{-\frac{4}{5} \phantom 1}=\frac{3}{5}: \left( -\frac{4}{5}\right)=-\frac{3\cdot 5}{5\cdot 4}=-\frac{3}{4}{\small.}\)
Таким образом, получаем:
\(\displaystyle 9\tg (3\pi-\alpha)=-9\tg \alpha=-9 \cdot \left(-\frac{3}{4}\right)=\frac{27}{4}=6{,}75{\small.}\)
Ответ:\(\displaystyle 6{,}75{\small.}\)