Егер \(\displaystyle \cos \alpha = -\frac{4}{5} \) және \(\displaystyle \alpha \in \left( \frac{\pi}{2};\ \pi \right) {\small}\) болса, \(\displaystyle 9\tg(3\pi - \alpha)\) табыңыз.
\(\displaystyle 9\tg(3\pi - \alpha)=\)
Өрнек үшін сәйкестендіру формуласын қолданамыз.
\(\displaystyle 3\pi-\alpha \) (\(\displaystyle 0<\alpha<\frac{\pi}{2} \) деп есептей отырып) бұрышының қай ширекте екенін анықтаймыз:
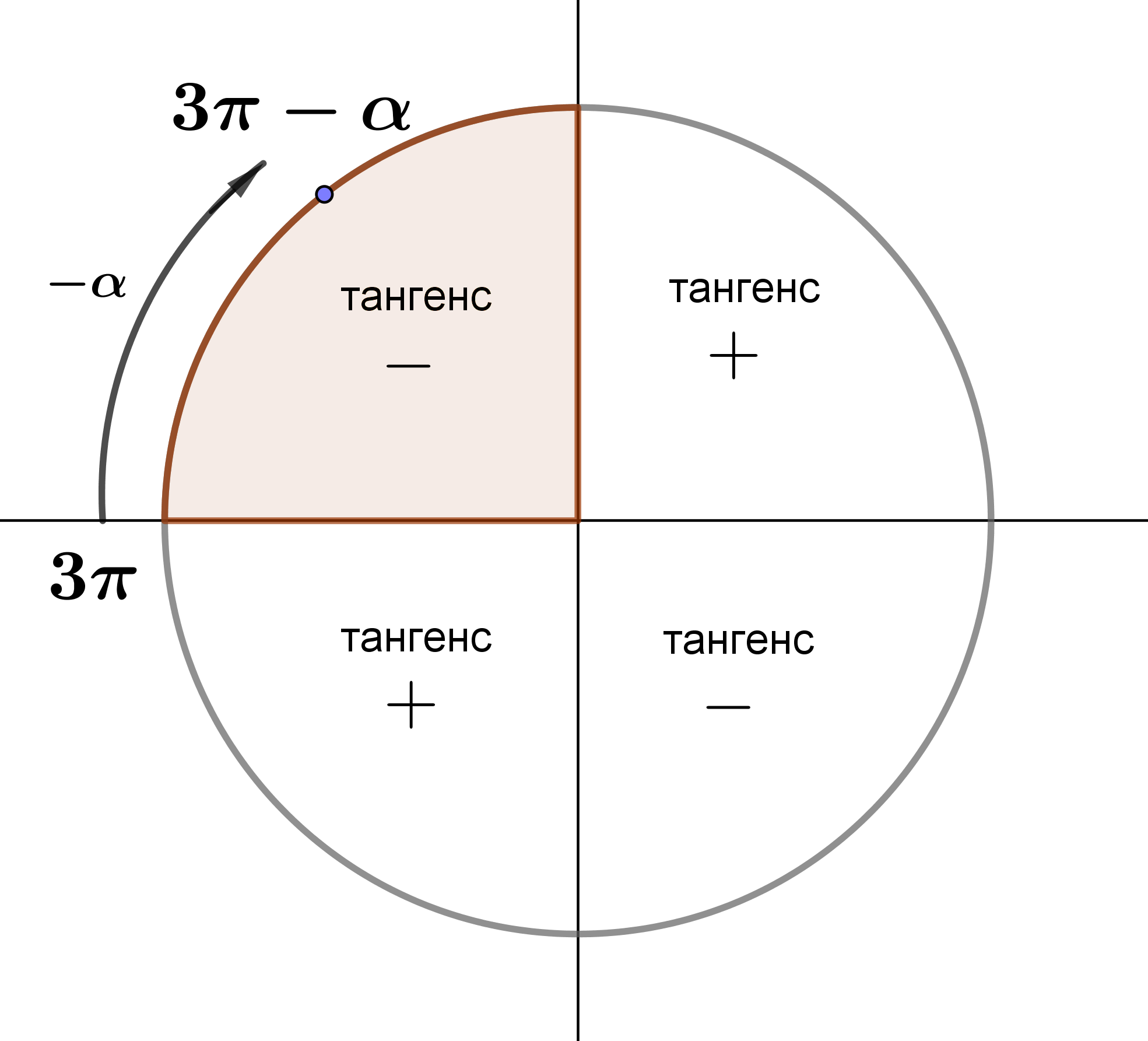
Екінші ширекте тангенс теріс.
Бірінші қосылғыш \(\displaystyle \pi k \) түрге ие болғандықтан, мұндағы \(\displaystyle k\) – тұтас, онда функция өзгермейді.
Демек,
\(\displaystyle 9\tg (3\pi-\alpha)=9(-\tg \alpha)=-9\tg \alpha{\small.}\)
Төмендегі формула бойынша \(\displaystyle \tg\alpha\) табамыз
\(\displaystyle \tg\alpha=\frac{\sin\alpha}{\cos \alpha}\)
Шарт бойынша \(\displaystyle \cos \alpha = -\frac{4}{5} \).
\(\displaystyle \sin\alpha{\small} \) табамыз.
Негізгі тригонометриялық тепе-теңдікті еске түсірейік.
\(\displaystyle \cos^2\alpha+\sin^2 \alpha=1\)
Осыдан аламыз
\(\displaystyle \sin^2\alpha=1-\cos^2\alpha{\small.}\)
Есеп шартында берілген \(\displaystyle \cos \alpha = -\frac{4}{5} {}\) мәнін қоямыз:
\(\displaystyle \sin^2\alpha=1-\bigg(-\frac{4}{5}\bigg)^2=1-\frac{16}{25}=\frac{9}{25}{\small.}\)
Егер \(\displaystyle \sin^2\alpha=\frac{9}{25}{ \small }\) болса, онда
\(\displaystyle \sin\alpha=\pm \sqrt{\frac{9}{25}},\)
\(\displaystyle \sin\alpha=\pm \frac{3}{5}{\small.}\)
\(\displaystyle \sin\alpha{\small}\) нақты қандай таңбаға ие екенін анықтаймыз.
Шарт бойынша \(\displaystyle \alpha \in \left( \frac{\pi}{2};\ \pi \right){\small.}\)
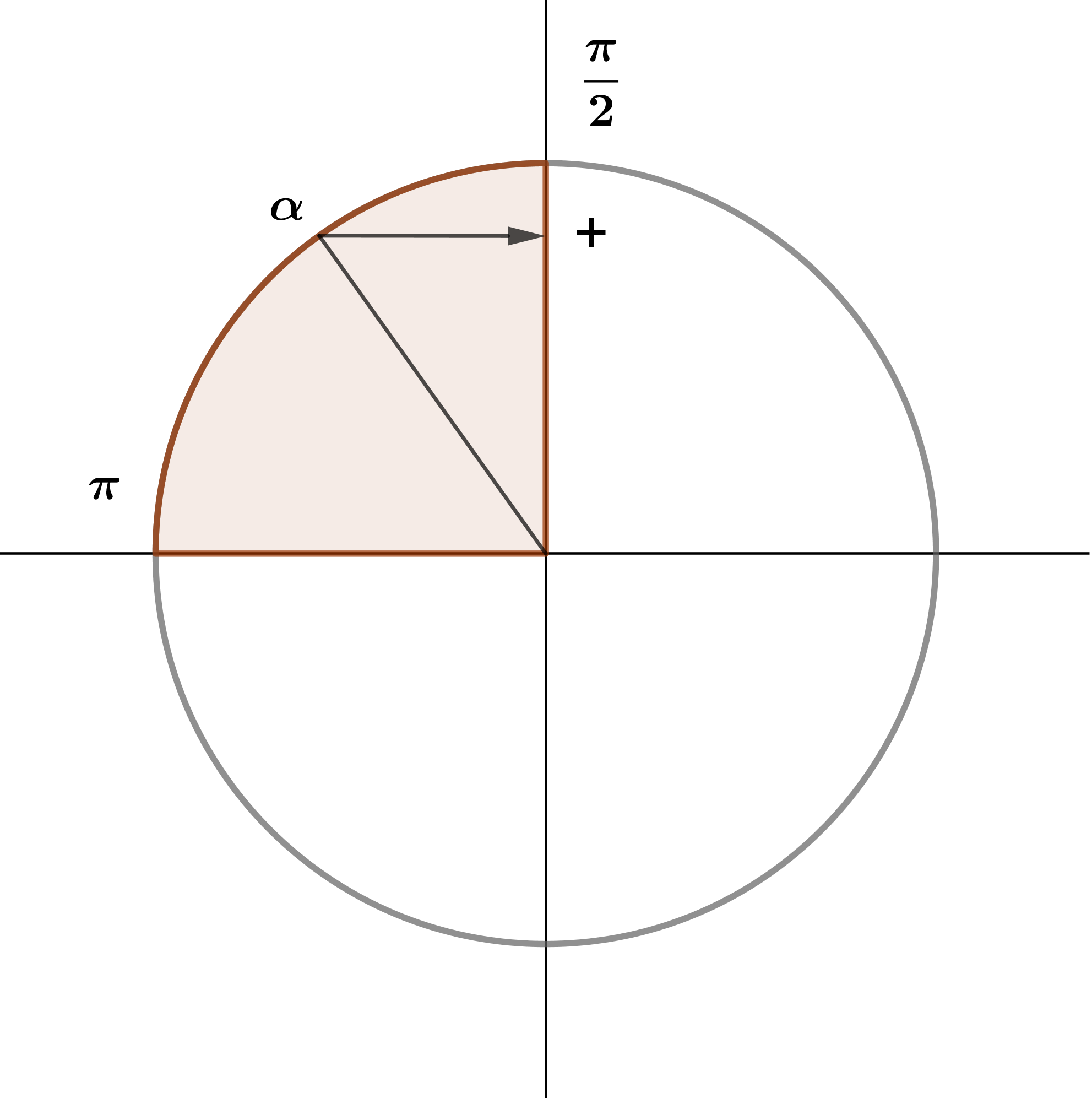
Екінші ширекте синустың мәні оң болады. Демек,
\(\displaystyle \sin\alpha=\frac{3}{5}{\small.}\)
Сонда:
\(\displaystyle \tg\alpha=\frac{\sin\alpha}{\cos \alpha}=\frac{\frac{3}{5}}{-\frac{4}{5} \phantom 1}=\frac{3}{5}: \left( -\frac{4}{5}\right)=-\frac{3\cdot 5}{5\cdot 4}=-\frac{3}{4}{\small.}\)
Осылайша, келесіні аламыз:
\(\displaystyle 9\tg (3\pi-\alpha)=-9\tg \alpha=-9 \cdot \left(-\frac{3}{4}\right)=\frac{27}{4}=6{,}75{\small.}\)
Жауабы:\(\displaystyle 6{,}75{\small.}\)