Егер \(\displaystyle \cos\alpha = \frac{\sqrt{10}}{10} \) және \(\displaystyle \alpha \in \big( \frac{3\pi}{2};\ 2\pi \big){\small}\) болса, \(\displaystyle \tg \alpha\) табыңыз.
\(\displaystyle \tg \alpha=\)
\(\displaystyle \tg\alpha=\frac{\sin\alpha}{\cos\alpha}\)
\(\displaystyle \cos \alpha{\small}\) мәні шарт бойынша берілген. Демек, \(\displaystyle \sin \alpha \) табу керек.
Негізгі тригонометриялық тепе-теңдікті еске түсіреміз.
Кез-келген \(\displaystyle \alpha\) үшін келесі дұрыс:
\(\displaystyle \cos^2\alpha+\sin^2\alpha=1{\small.}\)
Косинусты біле тұра, синусты табу керек. Келесіні аламыз:
\(\displaystyle \sin^2\alpha=1-\cos^2\alpha{\small.}\)
Есеп шартында берілген \(\displaystyle \cos \alpha = \frac{\sqrt{10}}{10} \) мәнін қоямыз:
\(\displaystyle \sin^2\alpha=1-\bigg(\frac{\sqrt{10}}{10} \bigg)^2=1-\frac{10}{100}=\frac{90}{100}=\frac{9}{10}{\small.}\)
Егер \(\displaystyle \sin^2\alpha=\frac{9}{10}\) болса, онда
\(\displaystyle \sin\alpha=\pm \sqrt{\frac{9}{10}}{\small,}\)
\(\displaystyle \sin\alpha=\pm \frac{3}{\sqrt{10}}{\small.}\)
\(\displaystyle \sin\alpha{\small}\) нақты қандай таңбаға ие екенін анықтаймыз.
Есеп шарты бойынша \(\displaystyle \alpha \in \left( \frac{3\pi}{2};\ 2\pi \right){\small.}\)
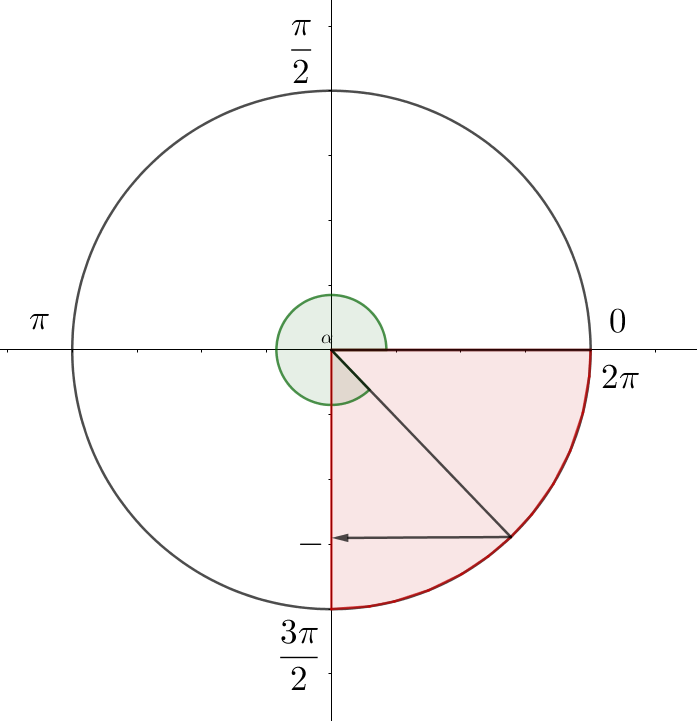
Төртінші ширекте синус мәні теріс болады. Сондықтан,
\(\displaystyle \sin\alpha=-\frac{3}{\sqrt{10}}{\small.}\)
Сонда
\(\displaystyle \tg\alpha=\frac{\color{blue}{\sin\alpha}}{\color{green}{\cos\alpha}}=\color{blue}{-\frac{3}{\sqrt{10}}}:\bigg(\color{green}{\frac{\sqrt{10}}{10}}\bigg)=-\frac{3 \cdot 10}{\sqrt{10} \cdot \sqrt{10}}=-\frac{3 \cdot 10}{10}=-3{\small.}\)
Жауабы: \(\displaystyle -3{\small.}\)