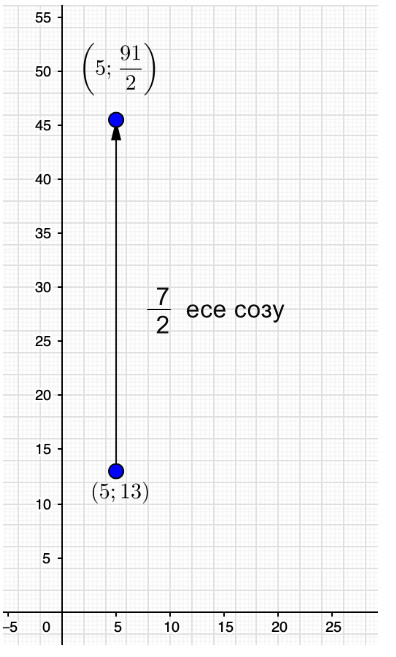
\(\displaystyle \rm OY\) осі бойымен \(\displaystyle \frac{7}{2}\) рет созылғаннан кейін \(\displaystyle (5;\, 13)\) нүктесінің координаттарын табыңыз.
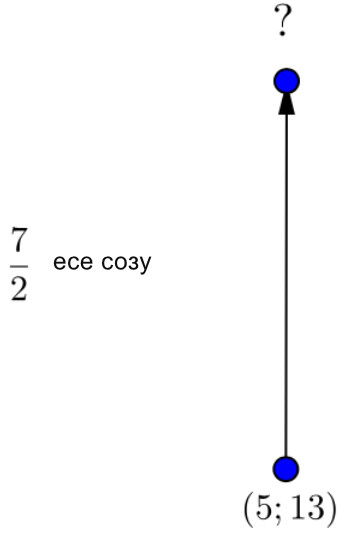
\(\displaystyle (x_0;\, \color{red}{ k}\cdot y_0)\) нүктесі егер \(\displaystyle \color{red}{ k}>1{\small }\) болса, \(\displaystyle (x_0;\,y_0){ \small }\) нүктесін \(\displaystyle \rm OY\) осі бойымен \(\displaystyle \color{red}{ k}\) есе созу арқылы алынған деп айтуға болады.
\(\displaystyle (x_0;\, \frac{y_0}{k})\) нүктесі егер \(\displaystyle 0<k<1{ \small }\) болса, \(\displaystyle (x_0;\,y_0){ \small }\) нүктесін \(\displaystyle \rm OY\) осі бойымен \(\displaystyle \frac{1}{k}\) есе созу арқылы алынған,
\(\displaystyle (x_0;\, \frac{y_0}{k})=(x_0;\, \frac{1}{k}\cdot y_0)\) және \(\displaystyle \frac{1}{k}>1{\small }\) болғандықтан.
\(\displaystyle \rm OY\) осі бойымен \(\displaystyle \frac{7}{2}\) есе созылу нүктенің \(\displaystyle y\) (ордината) координатасының \(\displaystyle \frac{7}{2}\) есе ұлғаюын білдіреді.
Демек,
\(\displaystyle (5;\, 13) \rightarrow (5;\, \color{blue}{\frac{7}{2}} \cdot 13)=\left(5;\, \frac{91}{2}\right){\small .}\)