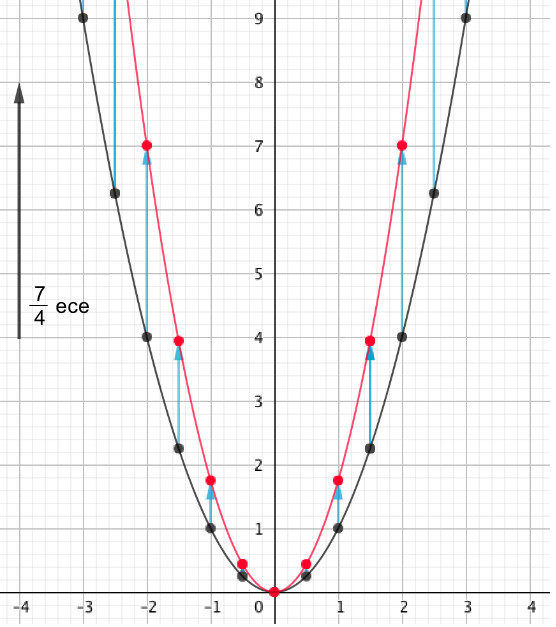
\(\displaystyle \rm OY\) осі бойымен \(\displaystyle \frac{7}{4}\) есе созылу арқылы \(\displaystyle y=x^2\) параболасынан алынған параболаның теңдеуін жазыңыз.
\(\displaystyle y=\)
Анықтаманы қолданайық.
Функция графигі
Жазықтықтағы \(\displaystyle y=\color{blue}{f(x)}\) функциясының графигі \(\displaystyle \{(x;\, \color{blue}{f(x)})| \, x\) анықтау аймағына жатады \(\displaystyle \}{\small }\) нүктелерінің жиыны деп аталады.
\(\displaystyle y=x^2\) параболасының графигі барлық нақты \(\displaystyle x{\small }\) сандары үшін \(\displaystyle \{(x;\, x^2) \}\) түрінің нүктелер жиыны болып табылады.
\(\displaystyle y=x^2\) параболасының графигін \(\displaystyle \rm OY \) осі бойымен созу дегеніміз - осы графиктің әр нүктесін \(\displaystyle \rm OY \) осі бойымен созу.
Демек, \(\displaystyle \{(x;\, x^2) \}\) нүктелер жиынынан әр нүктені алып, оны \(\displaystyle \rm OY{\small } \) осі бойымен созу керек.
\(\displaystyle (x;\, x^2)\) түрінің бір нүктесін алып, оны \(\displaystyle \rm OY{\small } \) осі бойымен \(\displaystyle \color{blue}{ \frac{7}{4}}\) есе созамыз, яғни ординатаның мәнін \(\displaystyle \color{blue}{ \frac{7}{4}}\) есе арттырамыз.
Егер осы \(\displaystyle (x;\, x^2)\) нүктесінің ординатасын \(\displaystyle \color{blue}{ \frac{7}{4}}\) есе арттырса, онда бұл \(\displaystyle (x;\, \color{blue}{ \frac{7}{4}} \cdot x^2){\small }\)координаттары бар нүкте болады:
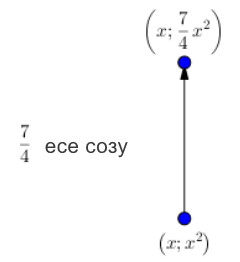
\(\displaystyle (x;\,x^2) { \small }\) түрінің әр нүктесімен осындай операция жасай отырып, \(\displaystyle y=\color{blue}{ \frac{7}{4}}x^2{\small }\) параболасының графигі болып табылатын \(\displaystyle \{(x;\, \color{blue}{ \frac{7}{4}}x^2) \}{ \small }\) нүктелерінің жиынын аламыз:
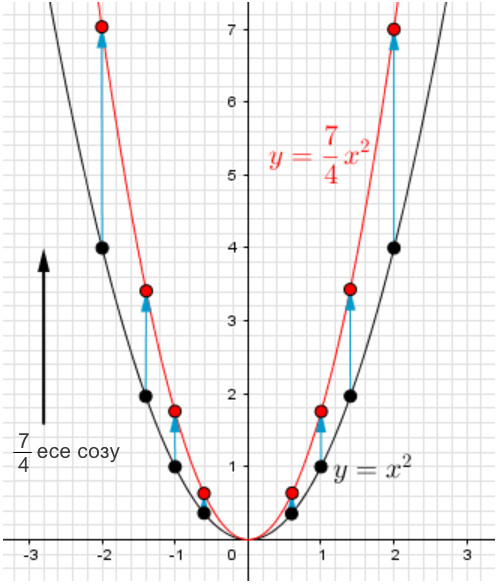
Жауабы: \(\displaystyle y=\frac{7}{4}x^2{\small .}\)