\(\displaystyle y=2x^2{\small }\) квадраттық функциясының графигіне сүйене отырып оның өсу мен кему аралықтарын табыңыз.
Для ввода \(\displaystyle \infty\) используйте меню дополнительного ввода.
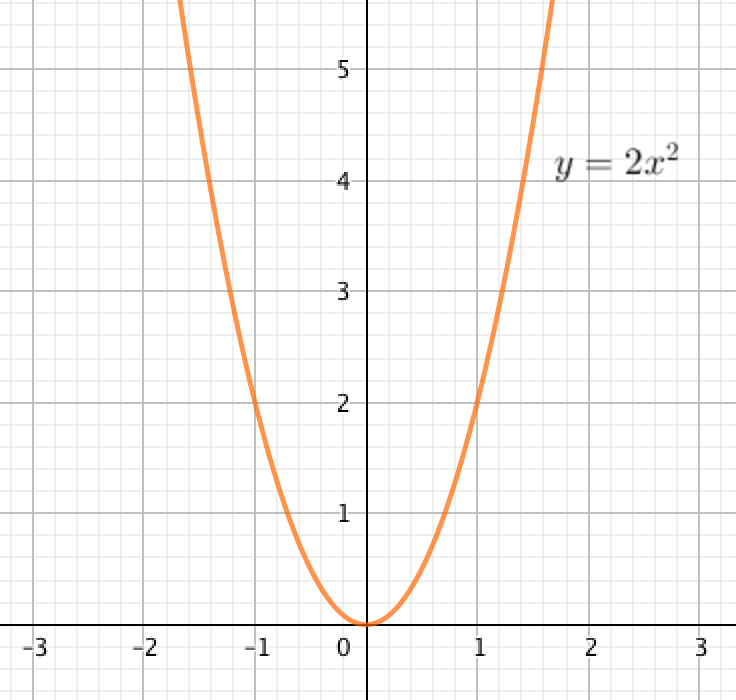
Функцияның өсуі және кемуі
\(\displaystyle y=f(x)\) функциясы \(\displaystyle x \in (a;\, b){\small }\) аралығында кемиді,
- егер осы аралықтағы үлкен \(\displaystyle x\) мәніне \(\displaystyle f(x){\small }\) функциясының кіші мәні сәйкес келсе,
- яғни кез-келген \(\displaystyle x_1,\, x_2 \in (a;\, b){\small }\) үшін, егер \(\displaystyle x_2>x_1{\small }\) болса, онда \(\displaystyle f(x_2)<f(x_1){\small .}\)
Графиктен көрініп тұрғандай
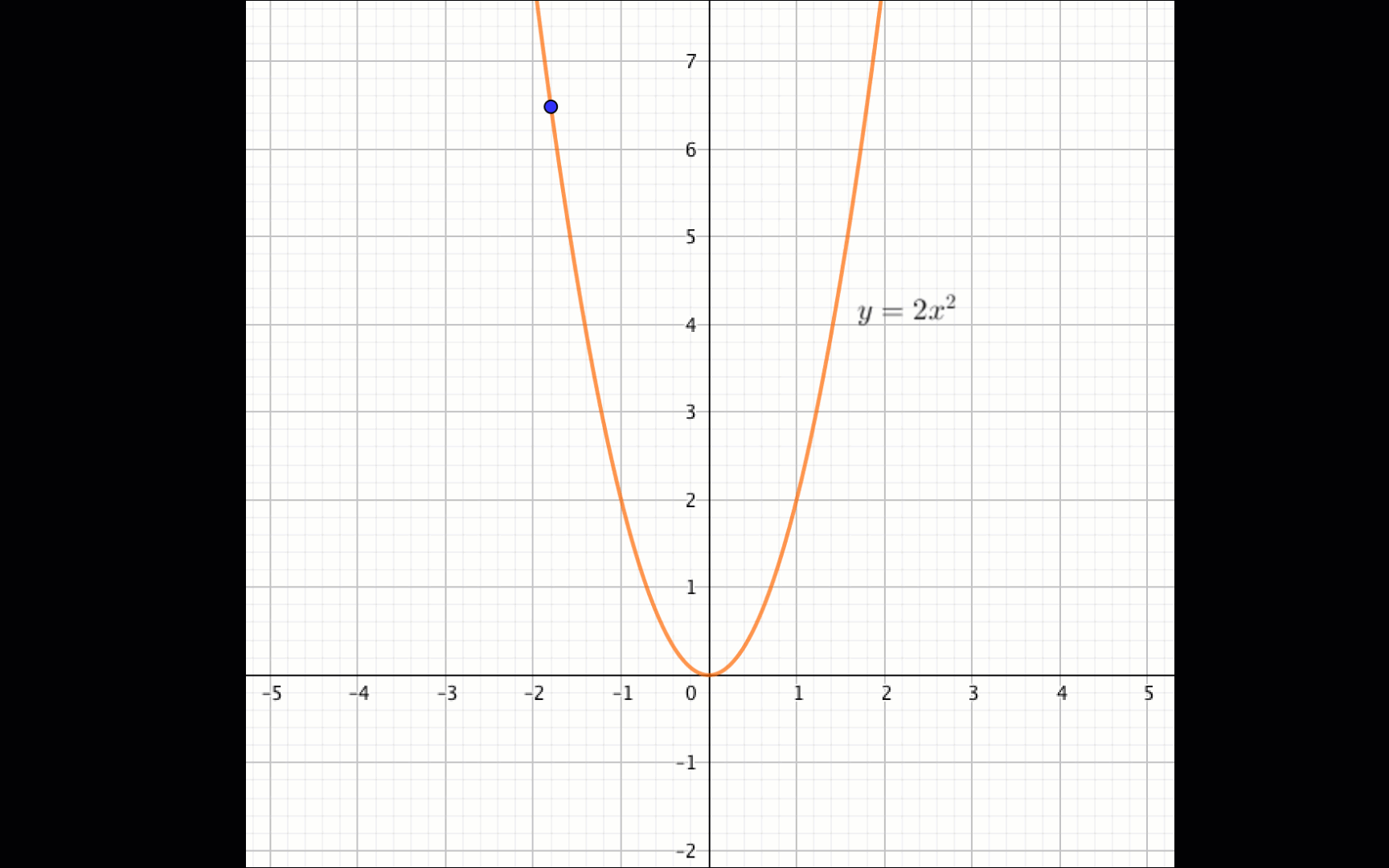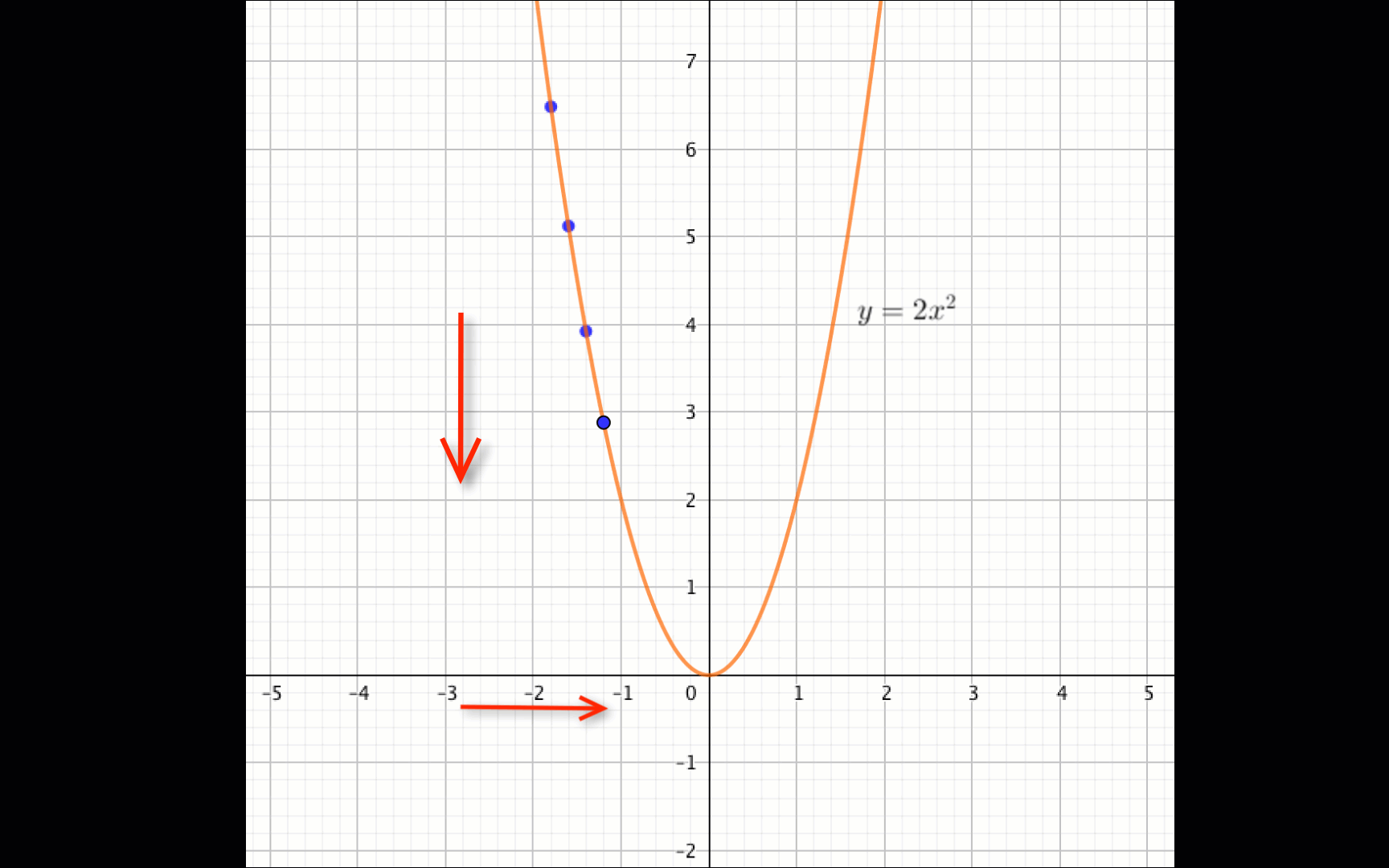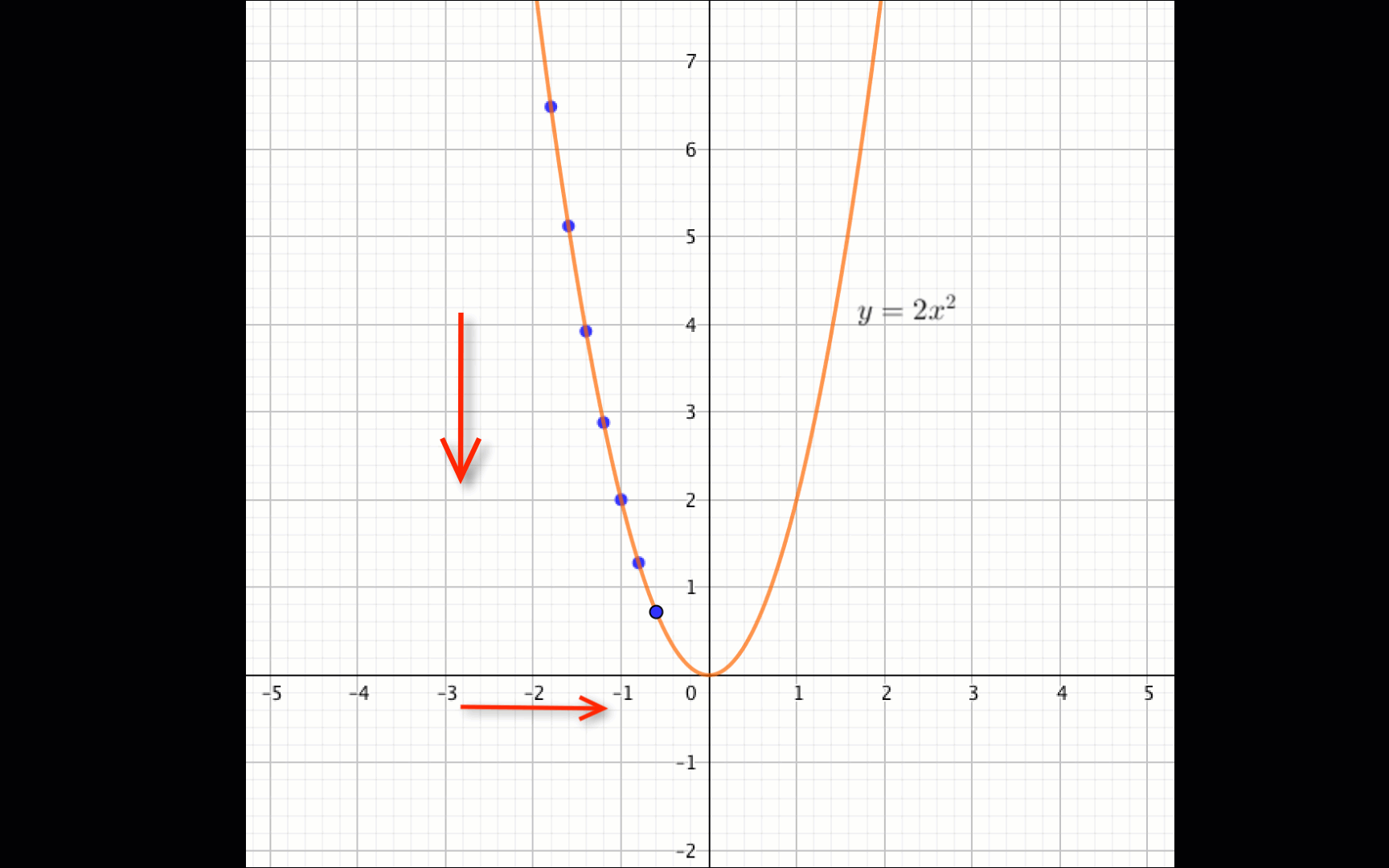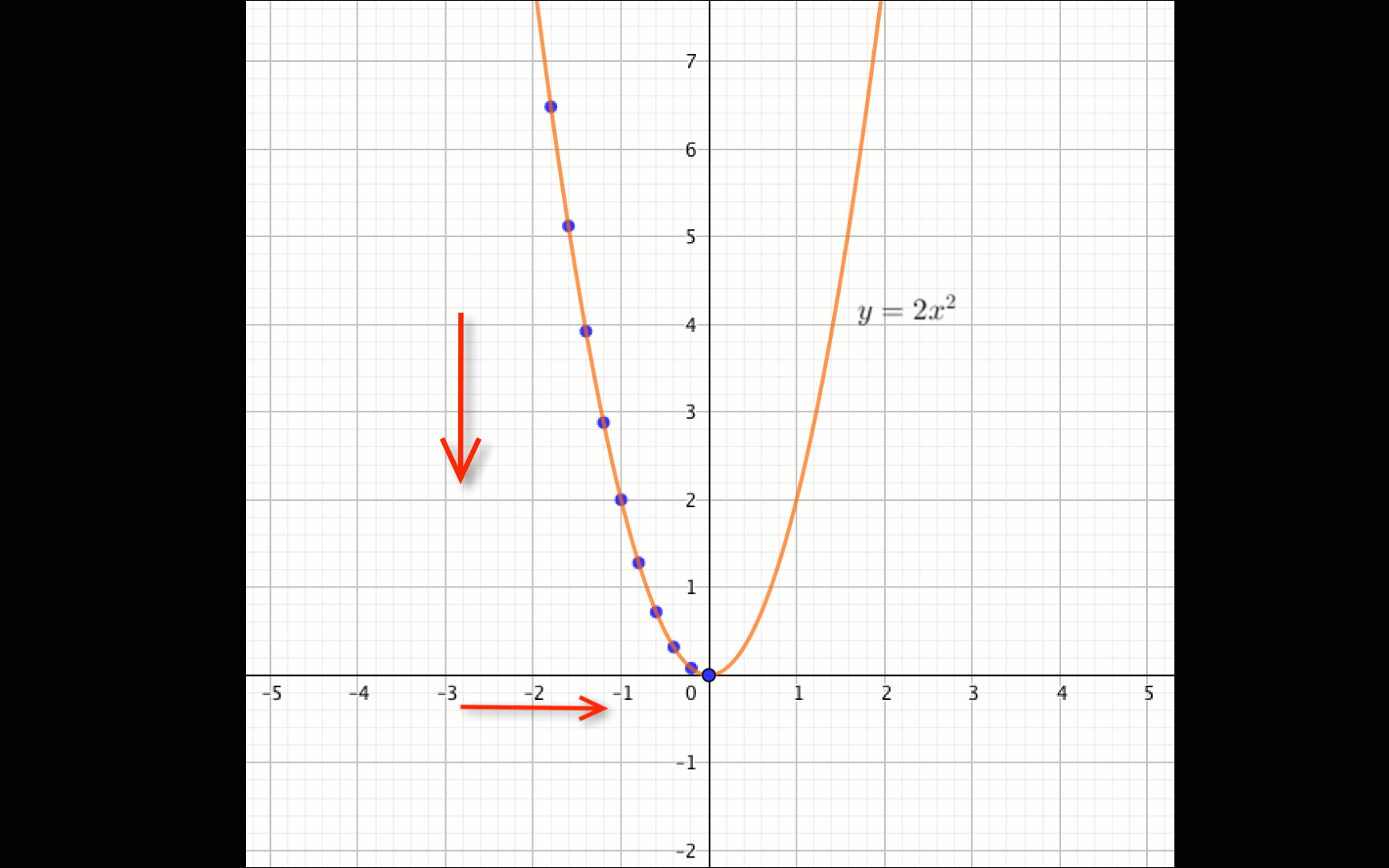
егер \(\displaystyle x \in (-\infty;\, 0){\small }\) болса, \(\displaystyle f(x)=2x^2\) функциясы кемиді.
Функцияның өсуі
\(\displaystyle y=f(x)\) функциясы \(\displaystyle x \in (a;\, b){\small }\) аралығында өседі.
- егер осы аралықтағы үлкен \(\displaystyle x\) мәніне \(\displaystyle f(x){\small }\) функциясының үлкен мәні сәйкес келсе,
- яғни, кез-келген \(\displaystyle x_1,\, x_2 \in (a;\, b){\small }\) үшін, егер \(\displaystyle x_2>x_1{\small }\) болса, онда \(\displaystyle f(x_2)>f(x_1){\small .}\)
Графиктен көрініп тұрғандай

егер \(\displaystyle x \in (0;\, +\infty){\small }\) болса, \(\displaystyle f(x)=2x^2\) функциясы өседі.