Тапсырма
\(\displaystyle y=-\frac{1}{2}x^2\) функциясының мәні ең үлкен болатын \(\displaystyle x\) координатын таңдаңыз.
Шешім
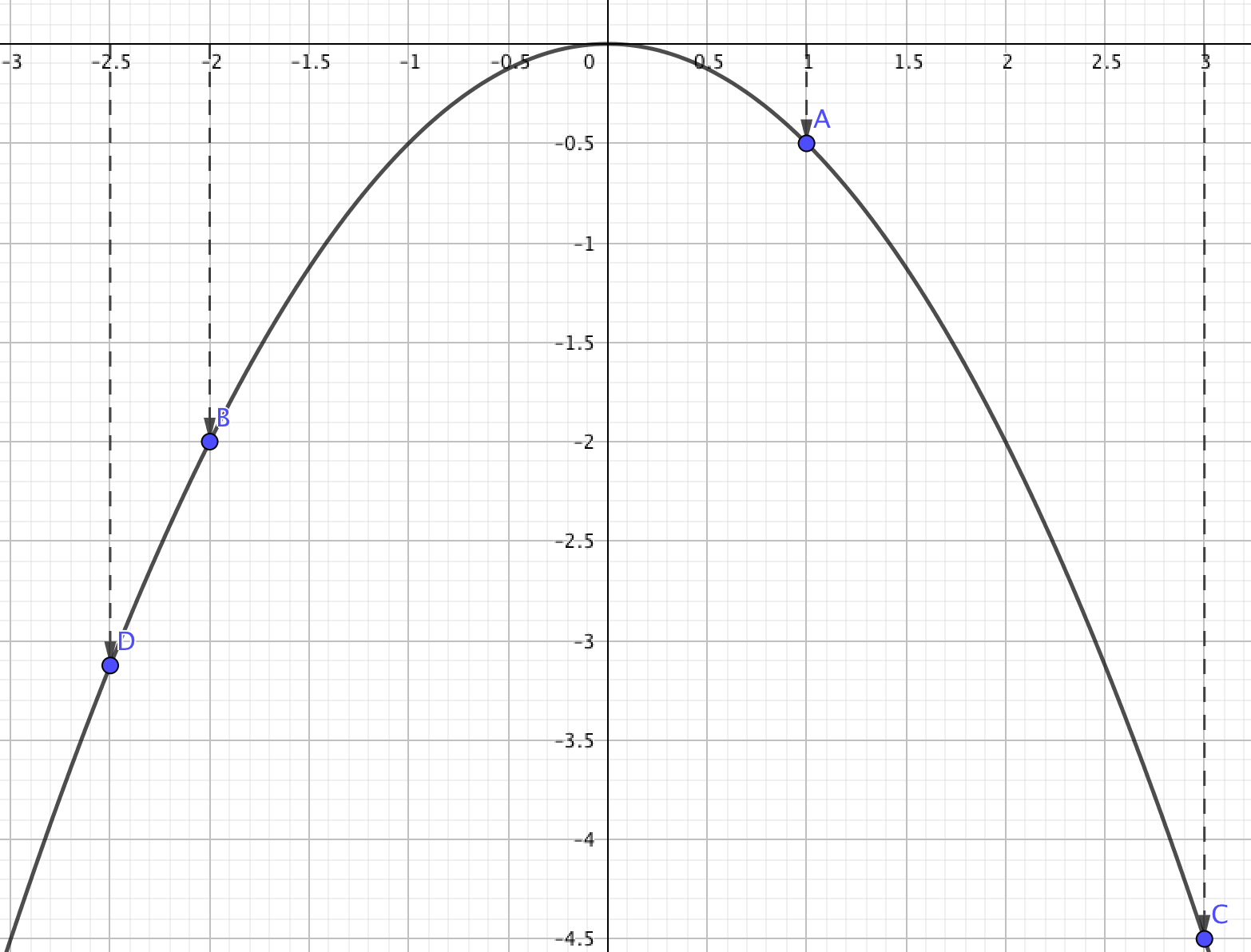
\(\displaystyle x=a\) нүктесіндегі функцияның мәні \(\displaystyle x=a\) координатасы бар берілген функцияның графигінде жатқан нүктенің \(\displaystyle y\) координатына сәйкес келеді.
Берілген нүктелердің әрқайсысының \(\displaystyle y\) координатасының орнын анықтайық:
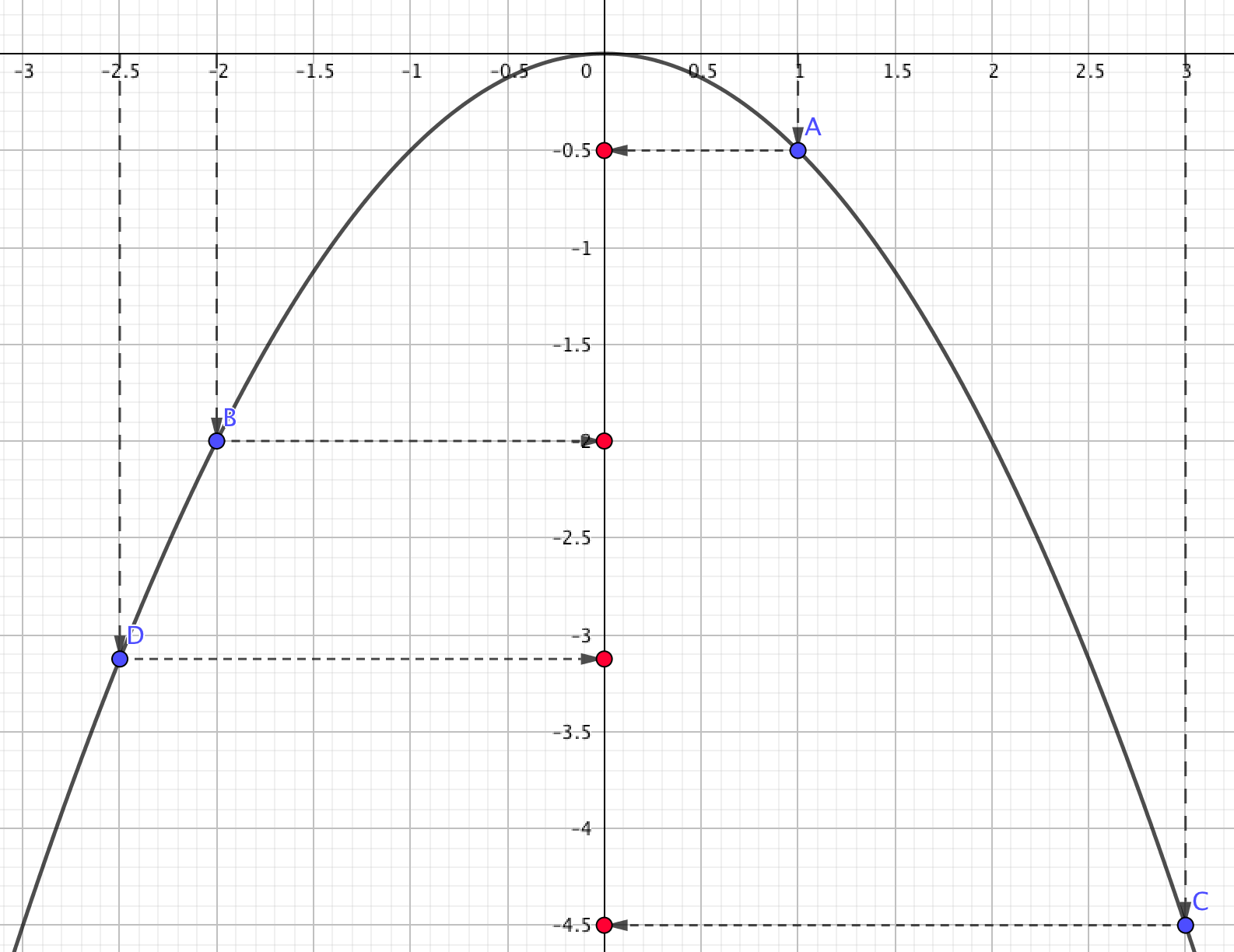
Сызбадан көрінетіні, \(\displaystyle y\) ең үлкен мәніне \(\displaystyle x=1\) координатасы бар нүкте ие болады.
Осылайша, \(\displaystyle x=1\) кезінде берілген \(\displaystyle x\) айнымалы мәндерінің ішінен \(\displaystyle y=-\frac{1}{2}x^2\) функциясының мәні ең үлкен болады.
Жауабы: \(\displaystyle x=1{\small .}\)