\(\displaystyle f(x)=12x^2+6x-6+\ln(x+1)^3{\small}\) функциясының анықтау облысын жазайық.
\(\displaystyle \ln((x+1)^{3})\) тек \(\displaystyle (x+1)^{3}>0{\small}\) ) болғанда ғана анықталғандықтан, анықтау облысы пішінге ие болады.
\(\displaystyle x> -1{\small.}\)
1) \(\displaystyle f(x)=12x^2+6x-6+\ln(x+1)^3{\small}\) функциясының туындысын табыңыз.
\(\displaystyle f^{\prime}(x)=\left(12x^2+6x-6+\ln(x+1)^3\right)^{\prime}=24x+6+\frac{3}{x+1}{\small.}\)
Жақшаларды ашамыз. Қосындының туындысы туындылардың қосындысына тең.
Яғни
\(\displaystyle \begin{aligned}\left(12x^2+6x-6+\ln(x+1)^3\right)^{\prime}=\left(12x^2\right)^{\prime}+(6x)^{\prime}+\left(\ln(x+1)^{3}\right)^{\prime}=\\[5px]=24x+6+\left(\ln(x+1)^3\right)^{\prime}{\small.}\end{aligned}\)
\(\displaystyle \ln(x+1)^3{\small}\) құрама функциясының туындысын табу керек.
Ережені қолдана отырып, оны кезең-кезеңімен орындайық.
ЕрежеКүрделі функцияның туындысы
\(\displaystyle \left(h({g(x)})\right)^{\prime}=\color{red}{h^{\prime}(g)}\cdot (\color{blue}{g(x)})'{\small.}\)
Әрбір кезеңнің міндеті \(\displaystyle h(g(x))\) функциясының туындысын қарапайым функцияның \(\displaystyle g(x){\small}\) туындысын есептеуге келтіру.
1-кезең. \(\displaystyle h(g(x))=\ln(x+1)^3{\small}\) деп белгілеңіз. Сонда:
\(\displaystyle\boxed{\begin{aligned}h(\color{blue}{g(x)})=\ln\color{blue}{(x+1)^3}\end{aligned}}\longrightarrow\) \(\displaystyle \boxed{ \begin{aligned}&h(x)=\ln(x)\\&\color{blue}{g(x)=(x+1)^3}\end{aligned}}\longrightarrow\) \(\displaystyle \boxed{\begin{aligned}&h^{\prime}(x)=(\ln(x))^{\prime}=\frac{1}{x}\\&\color{red}{h^{\prime}(g)=\frac{1}{(x+1)^3}}\end{aligned}} \longrightarrow\)
\(\displaystyle \longrightarrow\boxed{\begin{aligned}\left(\ln(x+1)^3\right)^{\prime}=\color{red}{\frac{1}{(x+1)^3}}\cdot\left(\color{blue}{(x+1)^3}\right)^{\prime}\end{aligned}{\small.}}\)
Алынған:
\(\displaystyle 24x+6+\left(\ln(x+1)^3\right)^{\prime}=24x+6+{\frac{1}{(x+1)^3}}\cdot\left({(x+1)^3}\right)^{\prime}{\small.}\)
Қарапайымырақ функцияның туындысын есептеуге көшеміз \(\displaystyle (x+1)^3{\small.}\)
2-кезең. \(\displaystyle h(g(x))=(x+1)^3{\small}\) деп белгілеңіз. Сонда:
\(\displaystyle \begin{aligned}\boxed{h(\color{blue}{g(x)})=(\color{blue}{x+1})^3}\end{aligned} \longrightarrow\) \(\displaystyle \boxed{\begin{aligned}&h(x)=x^3\\&\color{blue}{g(x)=x+1}\end{aligned}} \longrightarrow\) \(\displaystyle \boxed{\begin{aligned}&h^{\prime}(x)=(x^3)^{\prime}=3x^2\\&\color{red}{h^{\prime}(g)=3(x+1)^2}\end{aligned}} \longrightarrow\)
\(\displaystyle \longrightarrow\boxed{\begin{aligned}\left((x+1)^3\right)^{\prime}=\color{red}{3(x+1)^2}\cdot\left(\color{blue}{x+1}\right)^{\prime}\end{aligned}{\small.}}\)
Алынған:
\(\displaystyle 24x+6+{\frac{1}{(x+1)^3}}\cdot\left({(x+1)^3}\right)^{\prime}=24x+6+\frac{1}{(x+1)^3}\cdot{3(x+1)^2}\cdot\left({x+1}\right)^{\prime}{\small.}\)
Қарапайым функцияның туындысын есептеуге көшейік \(\displaystyle x+1{\small.}\)
3-кезең. \(\displaystyle \left({x+1}\right)^{\prime}=(x)^{\prime}+(1)^{\prime}=1+0=1{\small}\) болғандықтан мынаны аламыз:
\(\displaystyle \begin{aligned}24x+6+\frac{1}{(x+1)^3}\cdot{12(x+1)^2}\cdot\left({x+1}\right)^{\prime}=24x+6+\frac{1}{(x+1)^3}\cdot{3(x+1)^2}\cdot1=\\[5px]=24x+6+\frac{3}{x+1}{\small.}\end{aligned}\)
Сонымен \(\displaystyle 12x^2+6x-6+\ln(x+1)^3 \) функциясының туындысын алу процесі келесідей болады:
\(\displaystyle \begin{aligned}\left(12x^2+6x-6+\ln(x+1)^3\right)^{\prime}&=24x+6+\left(\ln(x+1)^3\right)^{\prime}=24x+6+\frac{1}{(x+1)^3}\cdot\left((x+1)^3\right)^{\prime}=\\[5px]&=24x+6+\frac{1}{(x+1)^3}\cdot3(x+1)^2\cdot(x+1)^{\prime}=24x+6+\frac{3}{x+1}{\small.}\end{aligned}\)
2) Тұрақты \(\displaystyle f^{\prime}(x)=24x+6+\frac{3}{x+1}{\small}\) таңбасының интервалдарын табыңыз
\(\displaystyle \left(-1;\,-\frac{3}{4}\right){\small,}\) \(\displaystyle \left(-\frac{3}{4};\,-\frac{1}{2}\right){\small,}\) \(\displaystyle {\left(-\frac{1}{2};\,+\infty\right)}\) – тұрақтылық интервалдары \(\displaystyle f^{\prime}(x)=24x+6+\frac{3}{x+1}{\small.}\)
Функцияны бөлшек түрінде қайта жазайық:
\(\displaystyle \begin{aligned}f^{\prime}(x)=24x+6+\frac{3}{x+1}=\frac{(24x+6)\cdot(x+1)+3}{x+1}=\frac{24x^2+24x+6x+6+3}{x+1}=\\[5px]=\frac{24x^2+30x+9}{x+1}{\small.}\end{aligned}\)
Осы рационал өрнектің алымының түбірін табайық.
Алымды \(\displaystyle 0{\small}\) мәніне теңестіріңіз
\(\displaystyle 24x^2+30x+9=0\,|\,:\,3{\small ,}\)
\(\displaystyle 8x^2+10x+3=0{\small .}\)
Мына квадрат теңдеуді шешейік.
Дискриминантты есептейік:
\(\displaystyle D=10^2-4\cdot 8\cdot 3=100-96=4\)
и
\(\displaystyle \sqrt{D}=\sqrt{4}=2{\small.}\)
Теңдеудің түбірлерін табайық:
\(\displaystyle x_1=\frac{-10+2}{2\cdot8}=\frac{-8}{16}=-\frac{1}{2}{\small,}\)
\(\displaystyle x_2=\frac{-10-2}{2\cdot8}=\frac{-12}{16}=-\frac{3}{4}{\small.}\)
Енді рационал \(\displaystyle \frac{2x^2+10x+12}{x+1}{\small}\) өрнектің бөлгішінің түбірлерін табайық
\(\displaystyle x+1=0{ \small ,} \)
\(\displaystyle x=-1{\small.}\)
Сан түзуіндегі туындының алымы мен бөлгішінің түбірін белгілеңіз. Бастапқы функцияның анықталу облысын ескере отырып \(\displaystyle x>-1{\small,}\) аламыз:
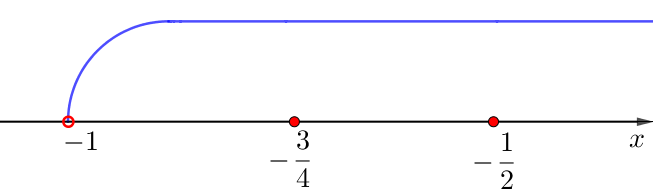
Сонымен, туындының тұрақты таңбасының интервалдары:
\(\displaystyle \left(-1;\,-\frac{3}{4}\right){\small,}\) \(\displaystyle \left(-\frac{3}{4};\,-\frac{1}{2}\right){\small,}\) \(\displaystyle {\left(-\frac{1}{2};\,+\infty\right)}{\small.}\)
3) Алынған интервалдар бойынша туындының белгілерін анықтайық.
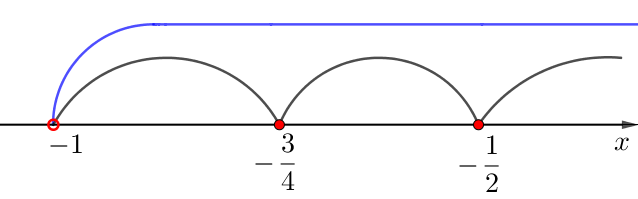
- \(\displaystyle \color{green}{\left(-1;\, -\frac{3}{4}\right)}\) және \(\displaystyle \color{Purple}{\left(-\frac{1}{2};\,+\infty\right)}\) аралықтарында \(\displaystyle f^{\prime}(x)>0{\small,}\)
- \(\displaystyle \textcolor{blue}{\left(-\frac{3}{4};\,-\frac{1}{2}\right)}\) функциясы \(\displaystyle f^{\prime}(x)<0{\small}\) интервалында
Функцияның таңбасын \(\displaystyle f^{\prime}(x)=24x+6+\frac{3}{x+1}\) аралықтардың әрқайсысында анықтайық:
\(\displaystyle \color{green}{\left(-1;\, -\frac{3}{4}\right)}{\small,}\) \(\displaystyle \color{blue}{\left(-\frac{3}{4};\,-\frac{1}{2}\right)}{\small,}\) \(\displaystyle \textcolor{Purple}{\left(-\frac{1}{2};\,+\infty\right)}{\small.}\)
Ол үшін интервалдардың әрқайсысынан нүктені таңдаймыз және осы нүктедегі функцияның таңбасын анықтаймыз. Аламыз:
\(\displaystyle \color{green}{x=-\frac{5}{6} \in{\left(-1;\,-\frac{3}{4}\right)}}\) белгісі үшін\(f^{\prime}\left(\color{green}{-\frac{5}{6}}\right)=24\cdot\left(-\frac{5}{6}\right)+6+\frac{3}{-\frac{5}{6}+1}=-20+6+18\color{red}{>}0{\small ;}\)
\(\displaystyle \color{blue}{x=-\frac{5}{8} \in \left(-\frac{3}{4};\, -\frac{1}{2}\right)}\) белгісі үшін
\(\displaystyle f^{\prime}\left(\color{black}{-\frac{5}{8}}\right)=24\cdot\left(-\frac{5}{8}\right)+6+\frac{3}{-\frac{5}{8}+1}=-15+6+8\color{red}{<}0{\small ;}\)- \(\displaystyle \textcolor{Purple}{x=0 \in{\left(-\frac{1}{2};\,+\infty\right)}}\) белгісі үшін\(\displaystyle f^{\prime}(\textcolor{Purple}{0})=24\cdot0+6+\frac{3}{0+1}=6+3\color{red}{>}0{\small .}\)
білдіреді,
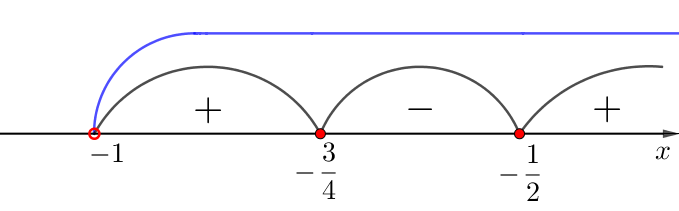
- \(\displaystyle \color{green}{\left(-1;\, -\frac{3}{4}\right)}\) және \(\displaystyle \color{Purple}{\left(-\frac{1}{2};\,+\infty\right)}\) аралықтарында \(\displaystyle f^{\prime}(x)>0{\small,}\)
- \(\displaystyle \textcolor{blue}{\left(-\frac{3}{4};\,-\frac{1}{2}\right)}\) функциясы \(\displaystyle f^{\prime}(x)<0{\small}\) интервалында.
Суреттегі туындының белгілерін белгілей отырып, біз аламыз:
4) \(\displaystyle f(x)=12x^2+6x-6+\ln(x+1)^3{\small}\) ережені пайдаланып функцияның өсу және кему аралықтарын анықтайық.
ЕрежеЕгер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар болса және \(\displaystyle f'(x_0)>0{\small}\) болса, онда
\(\displaystyle f(x)\) функциясы бүкіл интервалда \(\displaystyle (a;\,b){\small}\) өсуде ( seаrrow )
Егер кез келген нүкте үшін \(\displaystyle x_0\in(a;\,b)\) туынды \(\displaystyle f'(x_0)\) бар болса және \(\displaystyle f'(x_0)<0{\small}\) болса, онда
\(\displaystyle f(x)\) функциясы бүкіл интервалда \(\displaystyle (a;\,b){\small}\) кемуде ( serrow )
\(\displaystyle f'(x){\small}\) туындының белгілерін білу \(\displaystyle f(x){\small}\) өсу және кему аралықтарын анықтау
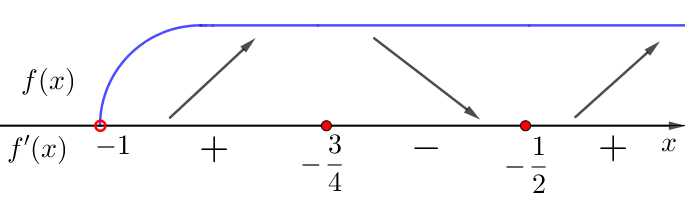
Схемалық түрде көрсетіңіз \(\displaystyle f(x){\small:}\)
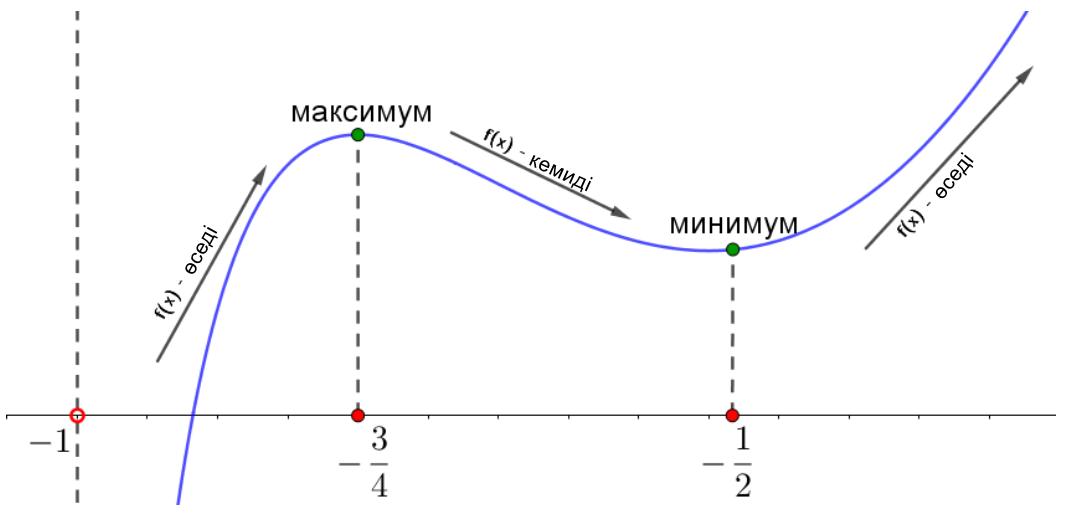
\(\displaystyle x=-\frac{3}{4}\) және \(\displaystyle x=-\frac{1}{2}\) нүктелері \(\displaystyle f(x){\small}\) облысына жатады.
Демек, \(\displaystyle x=-\frac{3}{4}\) – функцияның ең үлкен нүктесі \(\displaystyle f(x)=12x^2+6x-6+\ln(x+1)^3{\small.}\)
Ал\(\displaystyle x=-\frac{1}{2}\) – нүктесі ең кіші нүкте болып табылады.
5) \(\displaystyle \left[-0{,}9;\,0\right]\) аралық нүктелерінің қайсысында максималды мәнге жеткенін анықтайық.
Суреттегі \(\displaystyle \left[-0{,}9;\,0\right]{\small}\) интервалға назар аударыңыз
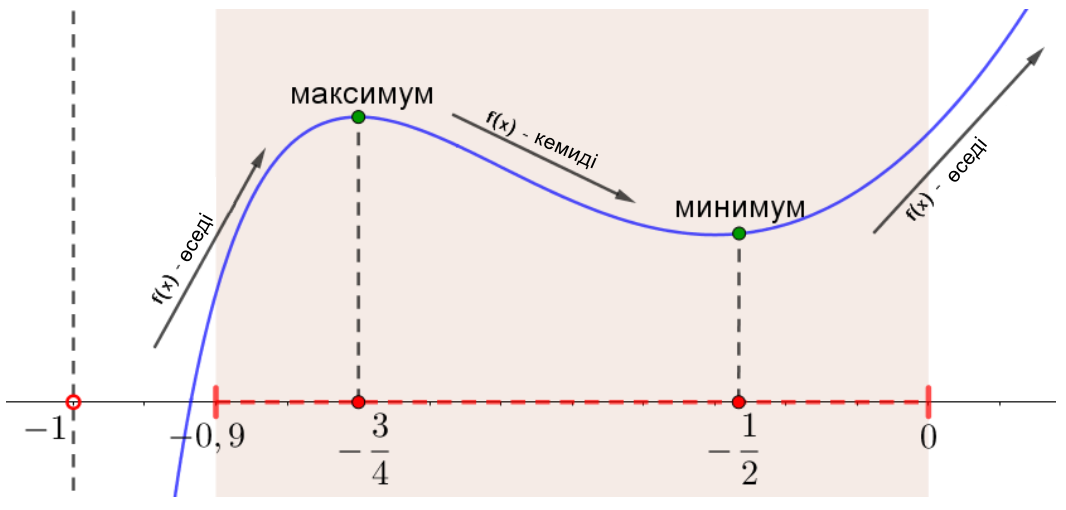
\(\displaystyle \left[-0{,}9;\,0\right]\) кесіндісінде \(\displaystyle f(x)\) функциясының максималды мәніне не максималды нүктеде \(\displaystyle \color{green}{x=-\frac{3}{4}}{ \small }\) немесе оң жағында \(\displaystyle \color{blue}{x=0}{\small }\) жететінін көруге болады
Осы нүктелердегі мәндерді есептеп, оларды салыстырайық:
\(\displaystyle \begin{aligned}&f\left(\color{green}{-\frac{3}{4}}\right)=12\left(-\frac{3}{4}\right)^2+6\cdot\left(-\frac{3}{4}\right)-6+\ln\left(-\frac{3}{4}+1\right)^3=\\[10px]=&6{,}75-4{,}5-6+\ln \left(\frac{1}{4}\right)^3=-3{,}75+\ln \left(\frac{1}{4}\right)^3=-3{,}75+\ln \left(4\right)^{-3}=\color{green}{-3{,}75-3\ln 4}{\small,}\end{aligned}\)
\(\displaystyle f(\color{blue}{0})=12\cdot0^2+6\cdot0-6+\ln(0+1)^3=-6+\ln1=-6+0=\color{blue}{-6}{\small.}\)
Өйткені \(\displaystyle 4>e{\small,}\) онда \(\displaystyle \ln 4 > 1 {\small}\) білдіреді,
\(\displaystyle \color{green}{-3{,}75-3\ln 4}<-3{,}75-3\cdot1=-6{,}75<\color{blue}{-6}{\small.}\)
Яғни, \(\displaystyle f\left(\color{green}{-\frac{3}{4}}\right)<f(\color{blue}{0}){\small.}\)
Демек, ең үлкен мәнге \(\displaystyle \color{blue}{x=0}\) нүктесінде жетеді және ол \(\displaystyle f(\color{blue}{0})=\color{blue}{-6}{\small}\) тең болады.
Жауабы: \(\displaystyle -6{\small.}\)

