Суретте \(\displaystyle y = f(x){ \small }\) интервалында анықталған \(\displaystyle (-4; 16){\small .}\) Функциясының туындысының графигі көрсетілген \(\displaystyle f(x)\) кесіндіде \(\displaystyle [0; 13]{\small}\) аралықтағы функцияның ең үлкен нүктелерінің санын табыңыз.
Есептің шартында \(\displaystyle [0; 13]{\small}\) кесіндідегі максималды нүктелер санын табу қажет
Сондықтан әрі қарай \(\displaystyle y=f^{\prime}(x)\) графигін тек \(\displaystyle [0;\, 13 ]{\small}\) интервалында қарастырамыз:
1. Графиктің \(\displaystyle \rm OX{\small}\) осін қиып өтетін нүктелерді суретте белгілеңіз
Біз мұны \(\displaystyle f^{\prime}(x)=0\) \(\displaystyle x=3\) және \(\displaystyle x=7{\small}\) нүктелерінен аламыз.
2. График интервалдарға бөлінеді, мұнда \(\displaystyle f^{\prime}(x_0)> 0\) және \(\displaystyle f^{\prime}(x_0)< 0{\small :}\)
\(\displaystyle (0;\,3)\) және \(\displaystyle (7;\,13)\) аралықтарында туынды оң \(\displaystyle (3;\, 7)\) аралықтарында туынды теріс болады.
3. \(\displaystyle f(x){\small}\) өсу және кему интервалдарын анықтайық
| Интервалдар | Туынды белгі | Функция әрекеті |
| \(\displaystyle (0;\,3){\small,}\) \(\displaystyle (7;\,13)\) | \(\displaystyle \color{green}{f^{\prime}(x)>0}\) | \(\displaystyle f(x)\) өсуде \(\displaystyle \color{green}{\nearrow}\) |
| \(\displaystyle (3;\, 7)\) | \(\displaystyle \color{blue}{f^{\prime}(x)<0}\) | \(\displaystyle f(x)\) азаюы \(\displaystyle \color{blue}{\searrow}\) |
4. \(\displaystyle f(x)\) кесіндісінде \(\displaystyle [0; 13]{\small}\) схемалық түрде бейнелеңіз.
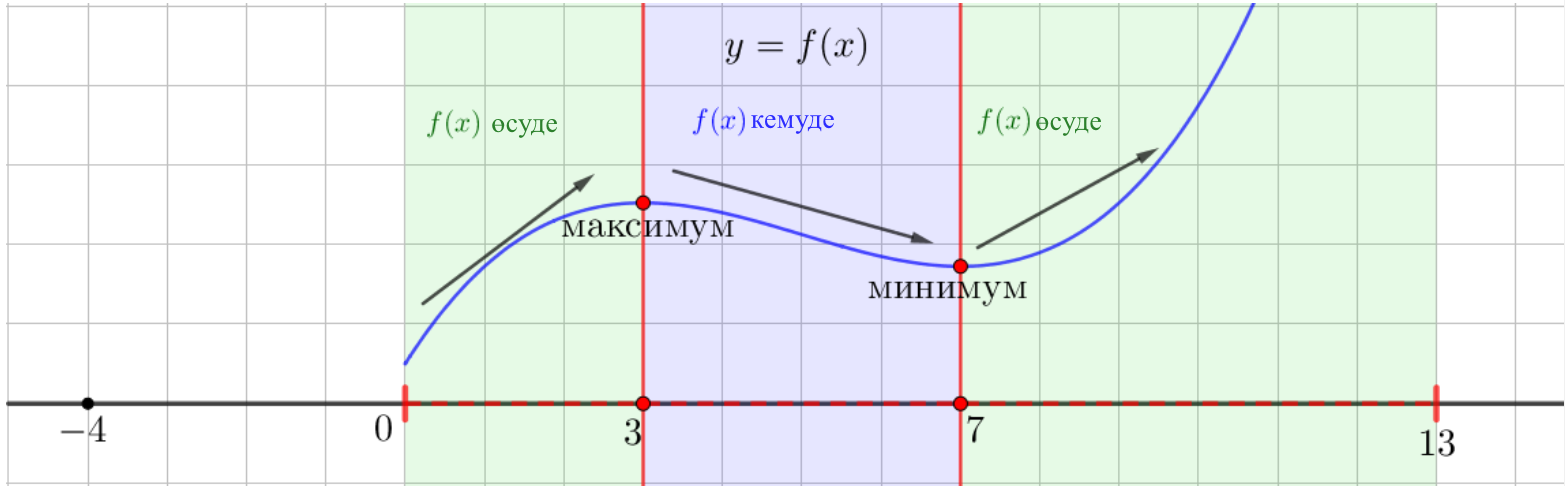
\(\displaystyle x=3\) нүктесі \(\displaystyle f(x)\) функциясының \(\displaystyle [0; 13]{\small}\) кесіндісіндегі жалғыз максималды нүктесі болып табылады.
Жауабы: \(\displaystyle 1{\small.}\)